1.经典力学中，角动量 
。量子力学中，轨道角动量算符 
是否仍有 
呢？
解：算符 
与 
的矢量积中，不出现有不对易因子 ， 
的项。例如，
，而
，
由于 
， 
，故
其他两个分量 
和 
也有类似的结果。
因而，在量子力学中仍有 
。
2. 质量为 
的粒子在中心力场
（1）
中运动，证明存在束缚态的条件为 
，再进一步证明在 
附近存在无限条束缚态能级。
证明： 当势能取式（ 1）时，根据维里定理，在任何束缚态中，有下列平均值关系，
， （2）
所以
（3）
由于 
，而束缚态 
，所以存在束缚态的条件为
（4）
在这个条件下，式（ 3）还可以写成
（5）
如能构造一个波包，其径向分布几率集中在 
附近的 
范围内，而且 
，则
（6）
只要 足够大， 
就可以小于任意指定正数，这样就得到无限多条密集在 
附近的能级。
另外，波包的构成必须受测不准关系的制约，
（7）
由于束缚定态 
，所以
（8）
（9）
由于 
必须小于 ，如 
，则对于足够大的 ，上式将给出 
，不能成为束缚态；反之，如 
，对于足够大的 ，式（9）中的第二项起主要作用，将给出 
，而且当 
， 
，各能级密集在 附近
3. 粒子在中心势场 
中运动，处于能量本征态
（1）
如果 
已经归一化，则势能平均值等于
（2）
试证明：如 为单调上升函数，即
，则对于任意给定的距离
，均有
（3）
证明：由于 是单调上升的，显然对于粒子的任何状态，总可以找到某个 
，使得
（4）
而且，当 
时， 
；当 
时， 
。因此，如 
，式（3）显然成立。如 
，则
但因
（5）
所以仍得
4. 对于氢原子的基态，求 
， 
，验证测不准关系。
解： 氢原子基态波函数为
(1)
宇称为偶。由于 
均为奇宇称算符，所有
（2）
由于 
各向同性，呈球对称分布，显然有
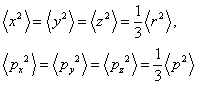（3）
容易算出
（4）
（5）
因此
（6）
（7）
（8）
测不准关系的普遍结论是
（9）
显然式 (8)和(9)是一致的，而且 
很接近式（9）规定的下限 
。
5. 以 
表示轨道角动量。证明：在 
的任何一个本征态下， 
和 
的平均值为 0。
证明：设 
为 的本征态，属于本征值 
，则
(1)
利用基本对易式
（2）
在 态下求平均值，即得
（3）
类似的，将对易式
在 态下求平均值，可证 
。
注意，在证明中只利用了角动量的基本对易式，并没有得到算符和波函数的具体构造式。因此，所得结论适用于任何一种角动量，即：在角动量 
的任何一个直角坐标分量 
的本征态下， 的另外两个分量 
的平均值均为 0。
6. 两个角动量耦合。当 
和 
给定时，相互独立的 
状态数为 
个。
(1) 以上结论是怎样得出的？
(2) 以 
为例，列出合成角动量量子数 j及 m的可能取值及相应状态数，验证之。
解：（ 1）当 给定时，
可能有 
个取值。当 
给定时， 
可能有 
个取值。因而
共有 
个，它们组成正交归一的完全系，时非耦合表象的基矢。
可由它们线性叠加为
因而，当 和 给定时，相互独立的 
的数目也是 个。
（2） 
时，a 可取值为 
时， 可取值为 
。
可取值为：
。由 
，故
当 
，对应 
个；
当 
，，对应 
个；
当 
，对应 
个；
对应 
数目总共正是 
个。