1．如何用矩阵表示量子态与力学量，并说明理由？

     答：矩阵表示一般用于本征值为离散谱的表象（相应的希尔伯空间维数是可数的）。

具体说，如果力学量 的本征矢为 ，相应本征值分别为 。假定一个任意态矢为 ，将它展开

则态矢 在 表象中波函数便可用展开系数的一列矩阵表示

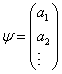
其意义是：在 态中， 取 的概率为 ，这与 表象中波函数意义是类似的。

力学量用厄米方阵表示

， 。

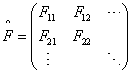显然，一列矩阵和方阵维数与希尔伯空间维数是相等的。

用矩阵表示力学量，有如下理由：

第一 可以反映力学量作用于一个量子态得到另一个量子态的事实。

设 ，式中 ， 。

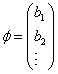取 ，

两端左乘 ，取标积得 ，

即

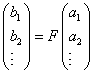
第二 矩阵乘法一般不满足交换率，这恰好能满足两个力学量一般不对易的要求。

第三 厄米矩阵的性质能体现力学量算符的厄米性。

对于本征值为连续谱的表象（希尔伯空间维数不可数），也可形式的运用矩阵表示，这时可将矩阵元素看成式连续分布的。

2.量子力学中，不同表象间：基矢 、波函数、力学量是如何变换的？
     答：量子力学中由一个表象到另一个表象的变换为幺正变换，它类似于欧氏空间中坐标转动。设 表象中的基矢为 表象中的基矢为

(1)  基矢变换关系为

式中 ，（ 为幺正矩阵）。

设有任意态 ，则态 在 及 表象中波函数分别为矩阵

。

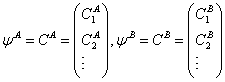(2) 波函数变换规则为：矩阵 。

(3) 力学量变换规则为： 。（式中 与 为力学量 在 、 表象中矩阵）

3.正变换有什么特征？

     答：幺正变换特点：

(1幺正变换不改变态矢的模，这一特征相当于坐标旋转变换；

(2幺正变换不改变力学量本征值；

(3)力学量矩阵之迹 TrF与矩阵行列式 dgtF亦不因幺正变换而改变．

4.  学量在其自身表象中如何表示？其本征矢是什么 ?

     答：如果力学量本征值为离散谱，那么，它在其自身表象中表示式为对角矩阵

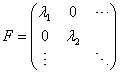， 为 诸本征值。

本征矢为单元素一列矩阵

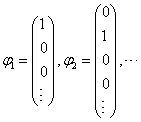
如果力学量 本征值为连续谱，则它在其自身表象中为纯变量

其本征矢为 函数。 ，对应本征值为 。

5.  力学量的矩阵对角化含义是什么 ?

     答：如果力学量 的矩阵 是非对角矩阵，则说明 不是 在其自身表象中表示，而是在某个其他表象 中的表示（表象 以力学量 的本征矢作为基矢）。所谓将矩阵 对角化，也就是将 转换到其自身的表象中来，这样做的目的是求矩阵 的本征值。

6．给定总能量算符 ，以 表示其本征值和本征函数，态矢量 a简记为 。

     答：按照海森伯运动方程，力学量算符 的时间变化率算符为：

（1）

定义能量表象中矩阵元

（2）

证明

（3）

其中

证明： 满足本征方程

（4）

其共轭方程为

式（ 1）两端取能量表象中矩阵元，即得

此即式（ 3）。

7．设 ，证明求和规则 。 （1）

     证明：利用算符 的海森伯运动方程，可得

(2)

取矩阵元，利用上题的结果，即得

（3）

再利用基本对易式

（4）

在能量本征态 下求平均值，即得

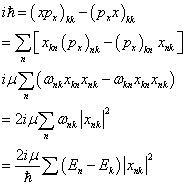
两端各乘 ，即得（1）式。
的另外两个分量 和 的矩阵元，显然也有同样的求和规则。注意，式(1)中 可以是任何一个特定的能级， 则遍及所有能级。