1．证明：非简并定态微扰中，基态的能量二级修正永为负。

     答：已知，微扰论中，对能量为 的 态，能量二级修正

如 态为基态，最低，在上式的取和中，的任一项均有 ，故 永为负。

2.证明：定态微扰论中，能量的一级近似是总哈密顿算符对零级波因数的平均值．

      答：设满足的正交归一化零级波函数以表出。已知 。则

正是能量一级近似.
3. 能级简并没有解除的解是否必定是近似解？反之，近似解是否必定是能级简并的？

     答：能级简并与波方程的近似解这两个概念的意义是不同的，没有什么直接的关联．我们知道，能级简并主要是由于体系哈密顿量具有某种对称性．只要保持这种对称以那么即使是精确解，其能级也是简并的．如氢原子．如果对称性受到彻底破坏或部分破坏，那么—般说来，简并应当消除或部分消除．应用微扰法求解定态问题时，得到的解一般均是近似解．非简并态微扰的近似解，能级当然是非简并的．简并态微扰法中由于微扰的作用．不管能级简并是否能解除，或解除多少，得到的解一般也是近似解．

4.一维谐振子，其能量算符为 (1)
设此谐振子受到微扰作用
(2)

试求各能级的微扰修正（三级近似），并和精确解比较。

      解： 的本征函数、本征值记为。如众所周知

（3）

在 表象（以 为基矢）中，的矩阵元中不等于0的类型为

（4）
因此，不等于0的微扰矩阵元有下列类型：

（5）

（6）

按照非简并态能级三级微扰修正公式，能级的各级微扰修正为：

（7）

（8）

（9）

本题显然可以精确求解，因为

令

可以写成

（10）

和式（1）比较，差别在于，因此的本征值为

（11）

因为 ，将作二项式展开，即得：

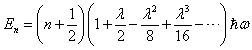（12）

和微扰论结果完全一致。

5. 氢原子处于基态．沿z方向加一个均匀弱电场，视电场为微扰，求电场作用后的基态波函数(一级近似)．能级(二级近似)，平均电矩和电极化系数．(不考虑自旋．)

     解：加电场前，基态波函数为

， （波尔半径） （1）

满足能量方程

（2）

其中

视外电场为微扰，微扰作势为

（3）

由于为偶宇称，为奇宇称，所以一级能量修正为0，

(4)
波函数的一级微扰修正满足方程

（5）

除了一个常系数外，即球谐函数，考虑到和都是球对称的，易知必可表示成

(6)

代入（5）式，并计及

其中

由式（5）可得满足的方程

（7）

为边界条件为处，。

用级数解法或试探法，不难求出式（7）的解为

（8）

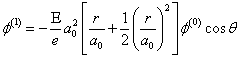因此 （9）

按照微扰论公式，能级的二级修正为 （10）

将式（3），（9）代入上式，即得

（11）

利用的具体表示式（1），容易算出

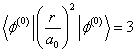
因此 (12)

此即外电场引起的基态能级移动，它和成正比．

电偶极矩算符为，其平均值为

（13） a

根据和的对称性，易得

，，

（14）

原子的极化系数由下式确定： 或 （15）

由此容易求得 （16）。