二、 计算题
1.在 ![]() 和
和 ![]() 的共同表象中,算符
的共同表象中,算符 ![]() 和
和 ![]() 的矩阵分别为
的矩阵分别为
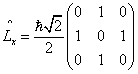 ,
, 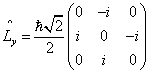 。
。
求它们的本征值和归一化本征函数,并将矩阵 ![]() 和
和 ![]() 对角化。
对角化。
2. 一维运动粒子的状态是
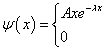
![]() 其中
其中 ![]() ,求
,求
( 1) 粒子动量的几率分布函数;(2)粒子的平均动量。
(利用公式 ![]() )
)
3. 设在 ![]() 表象中,
表象中, ![]() 的矩阵表示为
的矩阵表示为

其中 ![]() ,试用微扰论求能级二级修正。
,试用微扰论求能级二级修正。
4. 在自旋态 ![]() 中,求
中,求 ![]() 。
。
5. ![]() 和
和![]() 各是厄密算符。试证明,
各是厄密算符。试证明, ![]() 也是厄密算符的条件是
也是厄密算符的条件是 ![]() 和
和![]() 对易。
对易。
6. 在动量表象中角动量 ![]() 的矩阵元和
的矩阵元和 ![]() 的矩阵元。
的矩阵元。
7.求自旋角动量在 ![]() 方向的投影
方向的投影![]() 的本征值和所属的本征函数。
的本征值和所属的本征函数。
8.转动惯量为 ![]() ,电偶极矩为
,电偶极矩为 ![]() 的空间转子处在均匀电场
的空间转子处在均匀电场 ![]() 中,如果电场很小,用微扰论求转子基态能量的二级修正。
中,如果电场很小,用微扰论求转子基态能量的二级修正。
(基态波函数 ![]() ,利用公式
,利用公式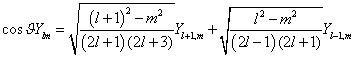 ) 。
) 。
9.证明下列关系式:
1. 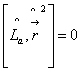 , 2.
, 2. 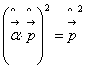
3. 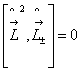 , 4.
, 4. 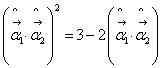
(其中 ![]() 为角动量算符,
为角动量算符, ![]() ,
, ![]() 为泡利算符,
为泡利算符, ![]() 为动量算符)
为动量算符)
10. 设 ![]() 时,粒子的状态为
时,粒子的状态为 ![]() ,求此时粒子的平均动量和平均动能。
,求此时粒子的平均动量和平均动能。
11. ![]() 为厄密算符,
为厄密算符, ![]() (
( ![]() 为单位算符),
为单位算符), ![]() 。(1)求算符
。(1)求算符 ![]() 的本征值;(2)在A表象下求算符
的本征值;(2)在A表象下求算符 ![]() 的矩阵表示。
的矩阵表示。
12. 已知体系的哈密顿量 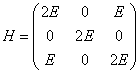 ,试求出(1)体系能量本征值及相应的归一化本征矢量。(2)将H对角化,并给出对角化的么正变换矩阵。
,试求出(1)体系能量本征值及相应的归一化本征矢量。(2)将H对角化,并给出对角化的么正变换矩阵。
13.一质量为m的粒子在一维无限深势阱中运动,
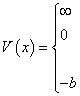
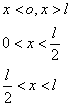 , b为小量,用微扰法求粒子的能级(近似到一级)。
, b为小量,用微扰法求粒子的能级(近似到一级)。
14.证明下列算符的对易关系。
1.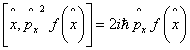
2.设算符 ![]() 与它们的对易式
与它们的对易式 ![]() 对易,即:
对易,即: ![]() ,证明:
,证明: 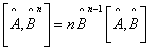
15.设有两个电子,自旋态分别![]() ,
, 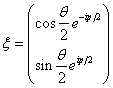 ,证明两个电子处于自旋单态
,证明两个电子处于自旋单态![]() 及三重态
及三重态![]() 的几率分别为:
的几率分别为: ![]() 。
。
16.求自旋角动量在 ![]() 方向的投影
方向的投影![]() 的本征值和所属的本征函数。
的本征值和所属的本征函数。
17.由任意一对已归一化的共轭右矢和左矢构成的投影算符 ![]() 。试证明(1)
。试证明(1) ![]() 是厄密算符;(2)有
是厄密算符;(2)有 ![]() ;
;
(3)![]() 的本征值为0和1。
的本征值为0和1。
18. 设在 ![]() 表象中,
表象中, ![]() 的矩阵表示为
的矩阵表示为 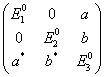 ,其中
,其中 ![]() ,试用微扰论求能级二级修正。
,试用微扰论求能级二级修正。
19.证明下列算符的对易关系:
1. ![]()
2.设算符![]() 与它们的对易式
与它们的对易式 ![]() 对易,即:
对易,即: ![]() ,证明:
,证明: ![]()
20.一体系由三个全同的玻色子组成,玻色子之间无相互作用。玻色子只有 两个可能的单粒子态。问体系可能的状态有几个?它们的
波函数怎样用单粒子波函数构成?
21.求证在 ![]() 的共同本征态下,角动量沿与z轴成
的共同本征态下,角动量沿与z轴成 ![]() 角的方向
角的方向 ![]() 的分量
的分量 ![]() 的平均值为
的平均值为![]() 。
。
22.证明如算符 ![]() 有共同的本征函数完备集,则
有共同的本征函数完备集,则 ![]() 对易。
对易。
23 .求