§11-3　感生电动势　涡旋电场

一　感生电动势

1.感生电动势的定义

导体不作宏观机械运动，而由导体所处的磁场随时间变化在导体内部产生的感应电动势，称感生电动势。

2.感生电动势产生的物理机制

　(1).感生电动势的产生不能由洛仑兹力进行微观解释

　　 例：无限长螺线管外线圈中的感生电流无法用洛仑兹力解释。

因螺线管外的磁场B=0，螺线管与线圈无相对运动。于是：

　　　　　　　　　

这与实验结果不相符合。

　　　结论：感生电动势是由与动生电动势不同的物理机制产生的。

　(2).感生电动势产生的物理机制——涡旋电场假设

麦克斯韦涡旋电场假设解释感生电场的逻辑思路

A.闭合电路中存在电流的前提条件是电路中存在电场

B. 闭合线圈中的磁通量发生改变时，线圈中存在感生电流

C. 变化的磁场将产生电场，且该感生电场是涡旋电场。

　结论：变化的磁场产生涡旋电场，涡旋电场的产生与变化磁场中是否存在导体无关。

3.感生电场、感生电动势的计算

感生电动势的产生仍然满足法拉第电磁感应定律：

对单匝线圈，法拉第电磁感应定律成为：　　

当线圈面积保持不变时，感生电动势为：　　

4.涡旋电场的性质

　　A.涡旋电场的散度或通量定理

　　　由于涡旋电场是封闭的闭合曲线，因此，通过任意封闭曲面的通量应满足：

　　或　　

结论：涡旋电场是无源场。

　　B.涡旋电场的旋度或环量定理

　或　

结论：涡旋电场是有旋场。

结论：涡旋电场是无源、有旋场。

思考题：比较静电场、动生电场、涡旋电场的基本性质

	静电场	动生电场	感生电场
散度
旋度
力场的性质	保守力场	保守力场	非保守力场

思考题：总结电场的性质

5.涡旋电场的应用举例

例：半径为R的圆柱形空间区域存在均匀磁场，当该磁场均匀

　　增加时

求：感生电场的空间分布。

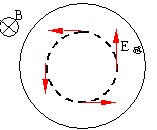
解：考虑到对称性及楞次定律，则，感生磁场大小的空间分布：

　　当r<R时：

当r>R时，所选取的回路包含的磁通量变化率为整个磁场：

　　　　　

例：在上例情形下，如果距圆心为h处有一导体

求：导体两端的感生电动势。

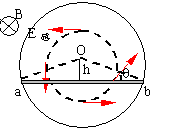
解法一：由上题结果，　　(时)

由楞次定律，可以判别a点比b点电势高。

解法二：本题也可以利用法拉第定律求解，即首先作辅助闭合回路oabo，由于oa、ob上没有感生电动势，因此，回路中的电动势就是ab上的感生电动势。最后根据楞次定律得到感生电动势的方向。

　　　　　　　　　　　　　　　　

用辅助回路方法的前提条件是辅助回路中的感生电动势易求或为0。