§11-5　磁场的能量

一　磁场的能量

1.磁场的能量

讨论磁场能量的思路：将磁场储能元件放置于电路中，那么，在时间t内，电场在其上消

　　耗的电能就应当等于磁场储能元件所储藏的磁场能量

为讨论问题方便起见，我们计算一个特例，然后将此结果作推广，得到任意情形下，磁场的储能公式。

特例：如图，计算线圈中储存的磁场能量

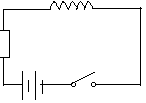
解：电源在dt时间范围内对线圈所做的功：

而，于是：

讨论：A.设线圈为无限长通电螺线管：，于是：。

B.将此结论推广，认为该结论对任意磁场储能都成立，那么，磁场储存的能量为：

　　　　　　　　　　　　　　　　　　　　

2.磁场的能量密度

　　　　　　　　　　　　　　　　　　　

　讨论：A.该公式对任意磁场储能都适用，即任意磁场储能都可以表示为：

　　　　B.利用磁场的能量密度可以计算磁场的总能量：

例：螺绕环的平均半径为R=8.0cm，截面积S=1.0cm²，线圈匝数N=1000

求：1.螺绕环的自感系数

　　2.若螺绕环通过的I=1.0A，其磁场能量和能量密度分别是多少。

解：1.螺绕环的半径远大于环的截面半径，此时，螺绕环的磁场可以看作为无限长螺线管

　　　产生的磁场。对应地，螺绕环的自感系数为：

　　　　　　　　　　　　　　　

2.螺绕环的磁场储能：　　　

　螺绕环的能量密度：　　　

讨论：对无限长螺线管或截面积很小的螺绕环，用本题的求解方法求解较为简单。也

　　　可以有公式：求解。

例：计算内外半径分别为R₁、R₂的同轴电缆单位长度的自感系数和磁场储能

解：能量密度：由安培环路定理，只有的区域中存在磁场分布：。

　　由　　　　　　　　

单位长度的能量：选择底面半径为r，厚度为dr，长度为l的体积元，该体积元的磁场

　能量为：

　令l=1，单位长度磁场的储能为：　　

单位长度的自感系数：　　由　

讨论：A.求解磁场储能的通常方法是首先求解磁场的分布，再求磁场的能量密度分布，

　　　　最后通过磁场的能量密度分布求解磁场的总能量。

　　　B.求自感系数通常有两种方法，一是由定义求解，另外就是通过能量求解。

例：设两线圈分别通以电流I₁、I₂。

求：1).解相邻两通电线圈的能量.

2).证明两线圈相互的互感系数相等

解：1).两线圈储存的磁场能量

　　分析：两线圈的储能是在它们电流没有达到稳定状态之前的过程中建立起来的。当两线圈的电流达到稳定状态时，磁场储存的能量不再因流过电流而发生改变。因此，计算磁场储能，只需考虑两线圈电流达到稳定前电流转化为磁场的能量。

为此，假设先给线圈1通以电流，当其从０达到I₁过程中，线圈1自身由于自感，必然在此期间将电能转化为磁场能量，即线圈1在此过程中储存的磁场能量为：

　　　　　　　　　　　　　　　　　

当线圈2通以电流时，除了线圈2的自感会将电能转化为磁场能外，线圈１对线圈2还有互感。保持线圈1的电流在线圈2电流从零增大到I2过程中始终不变，那么，电源1必然克服线圈1的互感电动势作功，从而又将一部分电能转化为磁场能。因此，在此过程中，电能转化为磁场能量的总能量值为：

　　　　　　　　　　　　　　　　　　

　　　　　

在上述两个过程中，电能转化为磁场能的总能量值为：

　　　　　　　　　

2).证明两线圈的互感系数相等

如果首先让线圈2通以电流I₂，然后保持I₂不变，再通以电流I₁，则与1)类似，系统储存的总能量为：　　　

显然，上述过程的最终状态完全相同，因而磁场储存的能量应当相同，于是：