二　惯性系下的相对运动理论

1.惯性系：牛顿定律严格成立的参照系，称为惯性系。

说明：对非惯性系，牛顿定律是不成立的，我们现在只限于讨论惯性系问题。

2.惯性系下的相对运动理论

　　 　　　　　

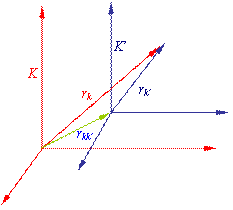
　　上式两边同时对时间求导

　　　　 即：　

同理：　

讨论：

(1).上述理论的适用条件：

A.只对惯性参考系成立

B.建立理论的基础是宏观、低速的牛顿时空观。

理由是在上述推理过程中，用到两个前提假设：一是认为在不同参照系下测得的位矢长度都相同(在k系和k’系测得的r_k’相同，否则，就不能应用平行四边形法则——平行四边形法则只能对同一参照系适用)；二是认为在不同坐标系下测得的时间都相同(否则就不能在等式两边同时对时间求导)。我们把这两个前提假设称为牛顿绝对时空观，相对论时空观则否认这两个基本假设。

(2).物理意义

A.绝对速度(绝对加速度)——将物体相对于静止参考系的速度(加速度)称为绝对速度(绝对加速度)。

B.相对速度(相对加速度)——将物体相对于运动参考系的速度(加速度)称为相对速度(相对加速度)

C.牵连速度(牵连加速度)——运动参照系相对于静止参考系的速度(加速度)称为牵连速度(牵连加速度)

于是，相对运动的物理意义可以理解为：

　　绝对速度=相对速度+牵连速度　　　　　　绝对加速度=相对加速度+牵连加速度

(3).应用方法：A.确定描述对象，选择静止参照系和运动参照系

B.确定绝对速度(绝对加速度)，相对速度(相对加速度)，牵连速度(牵连加速度)　

C.利用(2)~(4)或物理意义列方程并求解。

例：飞机罗盘显示飞机机头以速度215km/h向正东飞行，风速为65km/h，风速方向向正北

　求：(1).飞机相对地面的速度

　　　(2).飞机欲向正东飞行，机头应指向什么方位

　

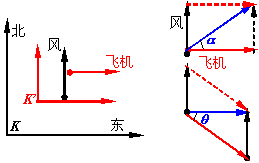
解法1：(1).飞机相对地面的速度

A.选择描述对象，确定静止参照系和运动参照系

描述对象：飞机；静止系：地面；动系：风

B.确定绝对速度，相对速度，牵连速度

　V_绝=飞机相对于地面的速度

　V_相＝飞机相对于风的速度=215km/h 正东

V_牵=风相对于地面的速度=65km/h　　 正北

C.利用公式物理意义列方程并求解。　由　　绝对速度=相对速度+牵连速度

　飞机相对地面的速度为：　　　　　

解法2：已知：，，求？

由相对运动速度合成公式：

(2).飞机欲向正东飞行，机头应指向什么方位

飞机欲向正东飞行，即飞机的绝对速度方向指向正东，相对速度、牵连速度不变，则：

　　　　　　　　　　　　　　　　

讨论：讨论相对运动问题的关键在于正确确定静止参照系、运动参照系，并准确确定三种速度，

作题时，一定按上述步骤求解，否则，很容易出错。

解法2: ， , , 求q ?

例：当自行车向正东方向以5m/s的速度行驶时，感觉风从正北向正南方向吹，当自行车速度增

　　加2倍时，感觉风从北偏东45^０方向吹来

求：风相对于地面的速度

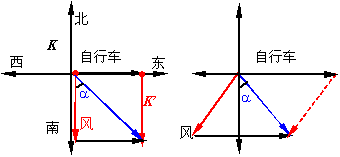
解：

设研究对象为风地面为绝对参照

系，自行车为相对参考系。

自行车向正东方向以5m/s的速度行驶时

v_绝=风相对于地面的速度(待求)

v_相=风相对于自行车的速度

v_牵=自行车相对于地的速度

，

自行车向正东方向以15m/s的速度行驶时：

　　　

联立求解上述四个方程得：　　　　　　　

解法2：请自己考虑