三　单缝夫琅和费衍射条纹位置的计算

1.菲涅耳半波带方法

将单缝某一衍射角的最大光程差(BC)用半个波长的长度去均分(CD，DE，EB)，对应的波面将单缝AB等分为AA₁，A₁A₂，A₂B，显然，AA₁，A₁A₂，A₂B具有相同的面积，因而在P点有近似相等的振幅(光强)。

相邻的半波带由于相位差相差p，因而在P点发生相消干涉而出现暗条纹。因此，当光程差为的偶数倍时，出现暗条纹，反之，光程差为的奇数倍时，由于最后一个半波带的光线没有被抵消，因而显现为亮条纹。介于两者之间的情况，则条纹亮度应为介于明暗条纹之间。

2. 明暗条纹的位置

　　（暗条纹）

　（明条纹）

3.光的强度分布

由上面分析，当条纹级别(k值)增大时，产生明条纹的半波带面积减小，因而光的强度减小，由振动合成的定量计算可知，绝大部分光的能量都集中于0级明条纹中，随着条纹级别的增大，光的强度迅速减小。

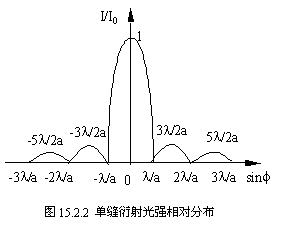
4.条纹宽度

角宽度：条纹对透镜L₂光心所张的角度，称为角宽度。明条纹的角宽度等于相邻两暗条纹中心间距离对L₂光心所张的角度，暗条纹的角宽度等于相邻明条纹中心间距离对L₂光心所张的角宽度。

中央亮条纹宽度：两个第一级暗条纹中心间的距离对L₂光心所张的角度。

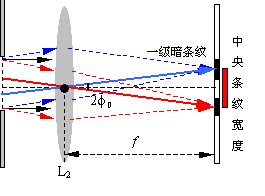
中央亮条纹的宽度：

由　　，（暗条纹）

中央亮条纹的角位置满足：

考虑到一般情况中衍射角度很小：

于是：

半角宽度为　　

设透镜的焦距为f，则中央亮条纹的线宽度为：

即，中央亮条纹的宽度为其他亮条纹宽度的两倍。

讨论：1.缝宽对衍射条纹的影响

　　波长保持不变时，中央明条纹线宽度与缝宽度成反比，称此规律为衍射反比规律。

当a增大时，中央明条纹的线宽度减小，表明第一级暗条纹(因而各级条纹)在向中央收缩，衍射现象变得不明显。当a>>l时，各级条纹收缩到中央明条纹中，衍射现象变得无法分辨，此时，光线通过缝的传播体现为直线传播。

　2.波长对衍射现象的影响

当缝宽保持不变时，中央明条纹的宽度因波长的不同而不同，用白光作衍射实验时，将出现彩色衍射条纹。

　3.k级条纹的线宽度

k级明(暗)条纹的角宽度，应等于k+1级暗(明)条纹中心与k-1级暗(明)条纹中心之间的距离对透镜光心所张的角度。

考虑到一般情况中衍射角度很小：　　

　　　角宽度为：　　　　　线宽度为：

例：已知Å，a=0.1mm，f=40cm

求：(1).中央明条纹的线宽度　　　　　　　　　　　(2).第一级明条纹中心的位置

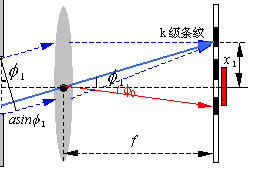
解：(1).由

可得：

(2).第一级明条纹出现的条件为：

　　同时　　

因此　

　

例：入射光为可见光，a=0.6mm，f=40cm，屏上距离中心O点x=1.4mm处P点恰为一明条纹,求：(1).该入射光波的波长

(2).P点条纹的级次

(3).从P点看，对该光波而言，狭缝处被分为多少个半波带？

解：由单缝衍射的明条纹公式

　　　　　　　　　　　　　　　（明条纹）

由于　a<<f，f很小，

于是　

在可见光范围内，当　k=3时，Å 此时，单缝处被分为7个半波带。

当　k=4时，Å　此时，单缝处被分为9个半波带。