三　光栅衍射理论——衍射光谱的光强及光谱位置

1.衍射光谱的光强计算

计算光栅衍射光谱强度的方法：认为光栅衍射光谱的强度由相距为d的多条狭缝光线的干涉与每一条宽度为a的狭缝的光线在空间某点的衍射光的强度叠加的结果。

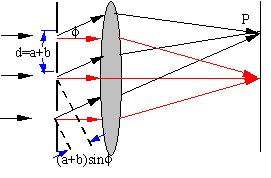
(1).N条相距为d的狭缝光线的干涉

显然地，这N条光线是同振幅、同频率、相位依次相差d的相干光。它们在P点的合成的合振幅为：

式中为每一缝在P点的振幅，d为相邻两束光在P点的相位差。

而　

令　

于是：　　　　

N条缝的光线在P点的合振动的光强为：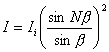　　　

(2).单缝光线在P点衍射光的强度：　　　　　　

其中，是每一条缝单独在屏中心()时的光强，

(3).光栅衍射光强计算公式

　　　　　　　　　　　　　　　

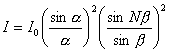
式中，称为单缝衍射因子，称为多光束干涉因子。

2.衍射光线的空间位置计算

　　明暗条纹出现的位置由光线的光强决定，光强取得极大值时，对应明条纹的位置，反之，则应是暗条纹出现的位置。

　　衍射光线明暗条纹的位置仍由N条狭缝光线的干涉与每一条缝的衍射两个因素决定。

(1).干涉因子对谱线位置的影响

　　因　　

讨论：A.由干涉因子决定的主极大位置

　　当或 ()时，由罗必塔法则

有　　　　　　　 　　且 　

即这些位置的光强为每条缝在该方向的N²倍，由可知，相邻两缝到达P点的相位是相同的，因此，P点谱线的光强取得极大值。极大值光强的强度与N²成正比。

B.由干涉因子决定的光强极小值位置(暗纹位置)

　当　，同时，时；或当　 　 (且)时，有。即此时，P点光谱的光强取得极小值，对应谱线为暗条纹。N愈大，相同衍射角区域出现暗条纹数目愈多，条纹愈细。由取得暗线的条件可知，在两条主极大谱线间，有N-1条暗谱线。

C.次极大谱线

当，时，有。即谱线光强介于主极大和极小值之间。由数学中的洛尔定理并考虑取得极小值谱线的条件，显然，在两条暗谱线之间，应当有一条谱线的光强取得极大值，但这条谱线光强不是主极大谱线的位置，或者说，这条谱线的光强虽然相对于两条暗线的光强取得极大值，但其光强远小于主极大谱线的光强，称之为次极大谱线。

两条暗线之间有一条次极大谱线，两条主极大谱线之间有N-2条次极大谱线。

(2).衍射因子对谱线位置的影响

　　由单缝衍射光强公式　

讨论：A.衍射因子对谱线的调制作用

显然，屏上任意一点光谱的光强值，不仅由干涉因子决定，同时受衍射因子的作用。衍射因子的作用体现为对干涉因子光强的缩小倍数的作用，常常称之为调制作用。

　B.衍射因子调制引起的缺级现象

当干涉因子取得主极大，同时衍射因子为0时，屏幕P点谱线的光强为0，并不出现主极大对应的亮线，此时，该主极大谱线不出现，称之为缺级现象。

缺级条件：由主极大条件　　　　　　

　　　　　衍射因子为0条件　　

两式相除，得到缺级条件：　　　　　　

式中，k为主极大谱线的级次。为单缝衍射暗条纹的级次。缺级情况由a,d决定。

小结：

1.当满足条件：——光栅方程时，干涉因子决定了光栅的主极大谱线位置，主极大光栅谱线的光强为：。

2.当满足条件： ()时，干涉因子决定了光栅的极小谱线位置，极小光栅谱线的光强为：。在两条主极大谱线间，有N-1条暗谱线。

3.当满足条件：，时，有。干涉因子决定了光栅的次极大谱线位置，两条暗线之间有一条次极大谱线，两条主极大谱线之间有N-2条次极大谱线。

4.当满足条件： ()时，会出现缺级现象。

5.光栅衍射光谱特点：在黑暗背景上出现明亮细窄亮条纹；N愈大，谱线愈细愈亮；谱线明暗程度受到衍射因子的调制。

例：已知Å，先后垂直入射到(1).500条/厘米的光栅　(2).10000条/厘米的光栅上。

求：分别经过每一光栅后第一级与第二级明条纹的衍射角。

解：设第一级、第二级明条纹的衍射角分别为，由光栅方程：，有：

　　　

(1).对500条/厘米的光栅

　　　　　　　　　　　　　　

(2).对10000条/厘米的光栅

　　　　　　　　　　　　　　(不存在)

可见，如果光栅单位长度中的缝数愈少，条纹角间距愈小，也愈不容易分辨。因此，一般实用光栅单位长度中的光栅缝数都较大。

例：已知Å，垂直入射一光栅上，测得第二级主极大的衍射角为30⁰，且第三级是缺级

求：(1).光栅常数。　(2).a的最小宽度。　(3).a,d确定后，屏幕上可能呈现的全部主极大的级次。

解：(1). 由光栅方程：可得：　

(2). 由缺级条件： 　()可得最小a值为：

　　　　　　　　　　　　　　

(3). 由光栅方程：可得：

当，时，。即，如果不出现缺级情况，屏幕上将出现这样7条主极大条纹。

由缺级条件： 　()可得：，即这些主极大条纹缺级，因此，实际出现的主极大条纹只有　这样5条主极大明条纹。