五　光栅的分辨本领

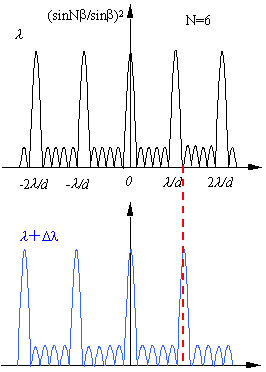
1.光栅衍射中光线能够分辨的瑞利判据：波长为l的谱线，如果与它的k级主极大最临近的光强极小位置刚好与波长为谱线的第k级主极大中心位置重合，则称这两条谱线是可分辨的。

2. 光栅分辨本领R的定义：　

3.光栅分辨本领的计算

A.波长为l的谱线对应的暗纹位置。

　由 ()可得：

B.波长为谱线第k级主极大中心位置。

　由可得：　　　　　

联立解上述两个方程有：

讨论：光栅的分辨本领与谱线的级次、光栅总缝数有关。

例：钠黄光的Å，钠双线波长差Dl＝6Å，用每毫米500条的光栅观察该线。

问：(1).光线以30⁰角倾斜入射光栅时，谱线的最高级次是多少？并与垂直入射情况相比较。

　　(2).如在第三级次恰能分辨出钠双线，光栅缝数必须为多少？

解：倾斜入射与垂直入射主要有两个区别，一是光程差不同，一是光的强度不同。本题不涉及计算光的强度，因而只需考虑光程差的区别。

(1).相邻缝同一衍射角光线的光程差为：

　　　

用它代替光栅方程中的相应光程差就得到倾斜入射时的光栅方程：

　　　

可能出现的最高级次的条件为：。

于是。　　　因此，可能出现的最高级次为k_max=5。

讨论：A.垂直入射时，由光栅方程：以及出现最高级次的条件：可得：　k_max<3.4 ，因此，k_max=3。

可见，倾斜入射可以看到更高级次的谱线。

　B.如果取虚线所示衍射光线，则光栅方程成为：，出现最高级次谱线的条件为：。

(2).由分辨本领计算公式：可得：N=327条，因此，光栅缝数至少为327条。