二　玻尔理论的应用与成就

1.系列常数的理论预期值与实验结果的符合程度，超过了人们的期望

(1). 里德伯常数

由(16.4-22)，里德伯常数的理论表述为：        　                   (16.4-22)

代入各物理常数值，可得里德伯常数的玻尔理论值为：  　    　　(16.4-26)

而氢原子的里德伯常数实验值为：                              (16.4-27)

两者的绝对误差为：　　　　　　　　　　          　                    (16.4-28)

　　可见，一方面，理论值与实验值两者符合得很好。另一方面，两者的误差又超过了当时实验精度所容许的误差范围(由表16.4-1，当时光谱实验的精度达到了1/10000)，玻尔认为这一误差可能来源于将核看作静止的假设(正因此，我们将此时的里德伯常数记为)。按(16.3-24)，将核静止假设改换为电子、核绕它们质心转动的坐标系只须将电子的质量用其折合质量代替。设作上述代替后任一元素A的里德伯常数记为，则：

　　　　　　　　　　　　                　　                             (16.4-29)

其中M、m分别为原子核、电子的质量。

由(16.4-26)，修正后的氢原子的里德伯常数的理论值为：   　　(16.4-30)

经过修正后的氢原子的理论值(16.4-30)与实验值((16.4-27)的绝对误差为：

　　　　　　　　　　     　　　　　       　　　　　　 (16.4-31)

理论值与实验值的符合程度超过了当时人们的预期，对其他原子作同样的计算，也有同样惊人的符合结果。

(2).玻尔第一轨道半径

在(16.4-24)中，令玻尔第一轨道半径为：                                (16.4-32)

则：　　　　　　　　　　                　                                   (16.4-33)

对氢原子的第一轨道半径（Z=1，n=1），r１＝a1，因此，a1是关于原子线度的重要物理量。代入各物理常数值，得：

　　　　　　　　　　　　　  　                                (16.4-34)

这与其他实验所得原子线度在数量级上是相同的。

(3).氢原子的基态能量

由   　　           　　                                   (16.4-23)

定义精细结构常数(其物理意义以后会清楚)：

　　　　　　　　　　　　　　

则氢原子的基态能量：　　　　　　　　　          　　　(16.4-35)

这与化学实验所得氢原子基态能量是相同的。

　　顺便指出，处于氢原子基态能级上的电子，对比其动能与式(16.4-35)，表明其轨道线速度与光速相比是很小的。因此，在通常情况下，我们在处理原子能级问题时并不考虑相对论效应。

 

2.玻尔理论成功解释了氢原子光谱和类氢离子光谱，并预言了氘的存在。

　　类氢离子是原子核外只有一个电子的原子体系。如He+，Li++，Be+++等。

　　将(16.4-22)、(16.4-23)代入(16.4-18)可得：

　　　　　　　　　　　　　　　　　　　　　         　　　　(16.4-36)

式中，Z为类氢离子的核电荷数，RA为类氢离子的里德伯常数，n、m取正整数，。

这样，由上式容易解释氢原子、类氢离子光谱线为什么具有确定波数或频率；为什么任何谱线均可以表述成为两光谱线之差以及不同谱线系为什么具有相同的光谱项等等。至于不同谱线系之所以能形成某一谱线系，玻尔理论认为，这是由于不同的末能级Em向同一初能级En跃迁的结果（如图16.4-2）。而由于末态与初态能级差不同，因而，谱线的频率自然也不同，表现为同一谱线系的谱线间间隔向短波方向递减等。

类氢离子与氢原子光谱有如上所述的类似之处，当然也有其特殊性：

A.考虑到类氢离子与氢原子在原子质量上存在差别，于是，RA与RH略有不同，因而与氢原子对应的光谱线波数必有微小差别。

B.类氢离子的核电荷数一定是氢原子的倍数，将(16.4-38)改写为类似氢原子的光谱公式，有：

　　　　　　　　　　　　　　　　　　　　　                  　　(16.4-37)

因此，与氢原子某一确定光谱线系相对应，类氢离子必然有氢原子谱线系中所没有的谱线，而这些谱线应在氢原子谱线系中两相邻谱线之间。

实践证明，类氢离子的谱线系的确具有上述性质，且定量地符合(16.4-36)。

 

例16.4-1：玻尔理论对“毕克林线系之迷”的解释

1897年，毕克林（Pickering）在天文观察时，发现一个很象巴尔末线系的谱线系（如图16.4-3），该谱线系具备如下两个特征：一部分谱线与氢光谱的巴尔末线系几乎重合，但又不完全重合；一部分谱线介于氢光谱巴尔末线系两相邻谱线之间。里德伯将毕克林线系归结为类似巴尔末的经验公式：

　　　　　　　　　　　　　　　　　　　　　　     　(16.4-38)


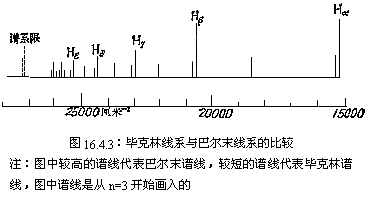
由于毕克林线系当时不能在地球上观察到，同时又与氢光谱相似，因而有人认为它就是星球上的氢光谱，只是星球上的氢不同于地球上的氢罢了。玻尔依据他的理论指出：毕克林线系不是天体上的氢发出的，而是He+发出的。很快，福勒依据玻尔的见解，在实验室仔细观察了He+光谱，结果证实这一光谱正是毕克林线系。当这一消息传到爱因斯坦那里时，爱因斯坦感到心悦诚服，并称玻尔理论是一“伟大发现”。

显然，依据(16.4-36)，对He+，立即可以得到(16.4-38)——玻尔理论的解释。

 

例16.4-2：氘存在的预言

1932年，尤雷(H.C.Urey)在实验中发现：在氢的线(6562.79Å)的旁边还有一条谱线(6561.00 Å)，两者只相差(1.79 Å)。他便假设这一谱线属于氢的同位素——氘(D)，并认为 ，然后计算RD、RH，进而计算相应的波长，结果发现，理论值与实验值很好符合。从而肯定了氘的存在（读者自己验算）。

事实上，原子光谱除了分离光谱以外，还有连续光谱。连续光谱的存在，并不否定原子中核外电子能级分裂的量子性。连续光谱形成的原因(以发射光谱为例)，可作如下解释：

设无限远处电子具有一定动能Ek，当其靠近原子核时，其能量可以表示为：

　　　　　　　　　　　　　　　　　           　　　(16.4-39)

当该电子被某一量子化轨道En俘获时，其能量降低，并向外辐射电磁波，由(16.4-16)：

　　　　　　　　　　　　　　                            (16.4-40)

由于初动能任意，因此，向外辐射的电磁波的频率可以是连续的。