三　惯性系和非惯性参照系

　1.相关概念

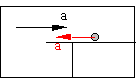
例：分别在加速行驶的火车、地面上观察火车车厢中水平桌面上的小球运动，必然得出的不同结论。

火车车厢上的观察者——小球没有受任何外力作用而产生了加速度——牛顿定律失效。而小球的运动情形，按惯性系中的牛顿定律，相当于小球受到的作用力为(以火车前进方向为正)。

地面上的观察者——火车车厢光滑的桌面不能提供小球作用力以使小球与火车以同样加速度运动，因而小球与地面保持相对静止——满足牛顿定律。

惯性系：牛顿定律严格成立的参考系，称之为惯性系。

非惯性系：牛顿定律不能成立的参考系，称之为非惯性系。

惯性力：在非惯性系中，为使物体保持相对静止，而必须假想给物体施加的作用力：

理解：A.惯性力是假想力，没有施力物体，也没有反作用力。是由于非惯性系造成的。

　　　B.惯性力的方向与非惯性系的方向相反，大小等于ma，可以理解为给非惯性系加上一个反方向的加速度，使之成为惯性系，而同时为保证物体与参照系的相对运动状态保持不变，因而必须给非惯性系中的每一个物体加上一个反方向的加速度，等效于给每个物体加上一个作用力——惯性力。

2.惯性系与非惯性系的区分

　　按惯性系和非惯性系的定义，通过实验，它们总是可以区分的。或者说，惯性系和非惯性系是具有不同性质的参照系，与运动的相对性无关。

3.非惯性系下的牛顿第二定律

　由惯性力的理解B，给物体加上反向加速度后，非惯性系就变为惯性系。那么，牛顿第二定律仍就适用，于是，在非惯性系中，牛顿第二定律可以改写为：

　　或　　　

　式中，是非惯性系的加速度，是物体相对于非惯性系的加速度。

例：加速上升的升降机内有一光滑斜面，求斜面上木块相对于地面和升降机的加速度。

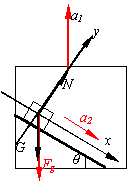
解：设升降机相对于地面的加速度为a₁，木块相对于升降机的加速度为a₂，选择升降机为参照系并建立图示坐标系。

给升降机加上反向加速度a₁后，对物体受力分析，如图，有：

　　　

解之得：　　(木块相对于升降机的加速度)

木块对于地面的加速度为：

，

　　　 (与斜面的夹角)

说明：上面解题过程中的F_g是惯性力，而是惯性力的反方向。

　　　该题也可以由非惯性系中的牛顿定律直接求解,给非惯性系加上反向加速度后进行受力分析，得到的加速度是相对于非惯性系的加速度。而不是相对于惯性系的加速度。

例：如图，斜面足够长，斜面B的质量为M，物体A的质量为m，A与B之间的摩擦系数为m，

斜面与地面之间无摩擦。

求：当物体 A在斜面上运行l时，斜面所发生的位移.

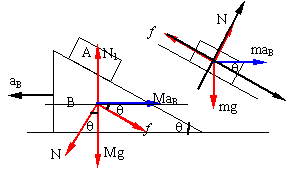
解：建立图示坐标系，给B施加反向加速度a_B使之成为惯性系。同时，设A相对于B的加速度为a_AB，于是，动力学方程为：

对A：

　　　

　　　

对B：

解此方程组得：　，

A物体在斜面上运行l：