三　动量定理的应用

1.可运用动量定理求解的问题特征

不考虑中间过程或中间过程很繁杂，而物体系状态量易求，或由物体系的状态量就可以求解的问题。

2.动量定理应用的常用近似方法

A.平均冲力：由于碰撞问题中作用力的时间一般很短暂，因而，在没有特别注明情况下，一般将碰撞过程中随时间变化的冲力视为平均力，即平均冲力。

B.忽略较小外力。一般情况下，冲力的大小比物体的重力、摩擦力等外力大一到二个数量级，因而，可以忽略重力、摩擦力等外力。

3.运用动量定理解题应注意的问题

A.动量定理的独立性、矢量性。

B.弹性碰撞、非弹性碰撞、完全非弹性碰撞问题

　弹性碰撞：碰撞后物体可以完全恢复形变的碰撞。弹性碰撞中动量、能量均守恒。

　非弹性碰撞：碰撞后物体不能完全恢复其形变的碰撞。在非弹性碰撞过程中，动量守恒，但能量不守恒。

完全非弹性碰撞：碰撞后物体不恢复其形变的碰撞。在完全非弹性碰撞过程中，动量守恒，但能量不守恒。且碰撞后物体结合在一体共同运动。

注：动量守恒与能量守恒一样，是自然界中成立范围最广泛的基本定理之一。迄今为止，没有发现动量守恒定理遭到破坏的事例。究其原因，动量守恒定理对应物理规律的平移不变性，即在平移情形下，物理规律的结构保持不变（或对称）。

C.解题步骤：a.确定研究对象，建立坐标系。

　　　　　　b.列动量定理或动量守恒方程，并求解。

例：一物体质量m=2kg, 受合外力(SI)的作用，初速度,

求：第1秒末物体的速度。

解：由动量定理的矢量独立性，分别在各坐标分量方向上应用动量定理：

完成积分得：

说明：本题的目的要求会应用动量定理矢量的独立性解题.

例：如图，用传送带A输送煤粉，料斗口在A上方高h=0.8m处煤粉自料斗口自由落在传送带A上。设料斗口连续卸煤的流量为q_m=40kg/s, 传送带A以v =3m/s的水平速度匀速向右运动.

求：卸煤的过程中，煤粉对传送带A的平均作用力的大小和方向。（不计相对传送带静止的煤粉质量，取g=10m/s²）

解：煤粉下落h时的速度 。

取在时间dt内落下的煤粉 dm=q_mdt 为研究对象，应用动量理，有：

平均冲力：

大小:|F|=200N，方向与x轴正方向成53.1^o

煤粉对传送带A的平均作用力与此力大小相等而方向相反。

例：一质量均匀分布的柔软的细绳铅直地悬挂着，绳的下端刚好触到水平桌面上。如果把绳的上端放开，绳将落向桌面。

试证明：在绳下落的过程中，任意时刻作用于桌面的压力，等于已落到桌面上的绳重量的三倍。

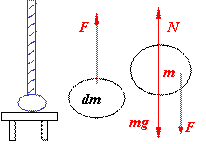
证：设绳的线密度为r。时刻t(下落h时)，绳的速度：

此时落在桌面上绳的质量为m=rh，m受三个个力的作用：重力mg、桌面的支持力N、落下绳的冲力F。由右下图可知

取时间t~t+dt内落下的绳为研究对象

（即压力是重量的三倍)。

例：如图，质量为M的物体有一个四分之一滑槽，静止在光滑水平面上，质量为m的滑块自其

顶部由静止开始下滑。

求：当m滑至滑槽底部时，M移动的距离。

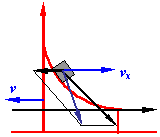
解：选择M、m为物体系，由于物体系在水平方向不受外力作用，因而动量守恒。

　　　　　　　　　

两边同时对时间积分：　　　

令：　　　　

于是： 　　　　　　　(1)

注意，v_x、s是相对于地面的水平速度和位移，相对于滑槽的水平位移为：

而　　　　　　　　　　

讨论：A.对中间过程是变力的运动过程，用牛顿定律求解，往往很繁杂，此时，应考虑用动量定理或动量守恒求解。

　　　B.求解过程中，并没有考虑m与M之间是否存在摩擦力，因而，即便存在摩擦力，上述结果同样成立。

　　　C.此题一个重要技巧用到(1)式，即两物体水平位移成比例。这在许多问题中经常用到。类似的还有速度、加速度成比例。

例：如图，A，B，C三物体质量均为M，B、C间由一长度为l₀的细绳连接，t=0时，B、C距离为0,桌面光滑。

求：(1).A、B运动后，经多长时间C开始运动？

(2).C刚开始运动时的速度

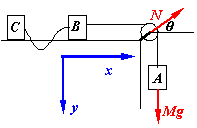
解：选择A、B、C为物体系，系统受到的外力有N、Mg

(1).由于系统受有合外力，因而系统动量不守恒。考虑到动量定理的矢量性和独立性以及合外力为恒力，在水平方向和竖直方向分别应用动量定理：

水平方向：　　　竖直方向：　　

合外力作用时间：　　以及　　　　　

联立求解得：　　　　　　

(2).C刚开始运动时的速度

C刚开始运动时，三个物体的速度应当相等。此时，相当于物体C与A、B两物体组成的系统相碰撞，在物体碰撞时，我们认为冲力远大于重力、摩擦力等内力，因此，可以忽略物体A所受的重力。设碰撞前后物体系的速度分别为v、V，由动量定理：

　　水平方向　　　　　

竖直方向　　　　　

与问题1的分析类似　 　

解此联立方程得：　　　　

讨论：A.用动量定理解题时，一个重要的问题是分清楚所研究的物体系对象，只有分清楚　　　　对象，才有可能正确确定内力和外力，否则，容易出错。如本题少分析N。

　　　B.用动量定理解题的另一重要问题是正确作近似，一般地，碰撞问题中的冲力比重　　　　力、摩擦力大，常常需要忽略。否则，就会出现约束条件不够的情况。如本题(2)。

　　实际上，本题之所以可以忽略重力，从理论上说，因为在绳的碰撞问题中，碰撞时间为0，因而冲力很大，可以忽略重力。

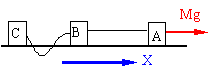
　　　C.本题进行模型转换后更容易求解，如图。

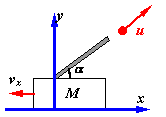
例：如图，光滑水平面上有一辆静止且质量为M的炮车，炮车的仰角为a，相对于炮车发射质量为m、出口速度为u的炮弹

求：(1).炮弹刚出口时，炮车的反冲速度

(2).若炮筒长为l，求炮弹发射过程中，炮车反冲的距离

解：该题有两个关键点：一是炮弹的速度是相对于炮车的速度，而不是相对于地面的速度；二是炮弹在炮筒中的运动是变速的，而不是匀速的。

(1).如图以地面为参考系建立坐标系，并以炮弹、炮车为研究对象，因此，在水平方向上动量守恒，由动量定理：

　　解得：　　　即炮车后退。

(2).设炮弹在炮筒中任意时刻的速度为u(t)，那么，此时对应的炮车速度为

　　

于是，炮车的反冲位移为：

故　　

说明：在质点系动量守恒问题中，如果涉及相对运动问题，那么，一定注意物体系中所有质点都必须相对于同一参考系。

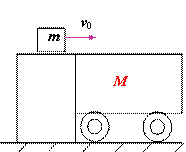
例：如所示，一辆质量为M的平顶小车静止在光滑的水平轨道上，今有一质量为m的小物体以水平速度v₀滑向车顶。设物体与车顶之间的摩擦系数为m

求：(1)从物体滑上车顶到相对车顶静止需多少时间？

(2)要物体不滑下车顶，车长至少应为多少？

解：(M+m):水平方向不受外力，动量守恒 （式中v是相对静止时的速度）

1).对物体m应用动量定理，有 解得：

2).物体m的加速度 a= -mmg/m=-mg。设车长至少为S，

则由：　v²-v₀²=2aS 得： S= (v²-v₀²)/2a= M(M+2m)v₀²/(2mg(M+m)²)

　 这个结果对吗？

错误。因为用牛顿定律求出的加速度a是相对惯性系—地面而速度v、v₀也是相对地面的，故由公式v²-v₀²=2aS求出的S当然也应是物体相对地面的运动距离，而不是相对非惯性系(车顶)的运动距离。

正确解法是先求出小物体m相对地面运动的距离

再求出小车M相对地面前进的距离

车的最小长度：

例：光滑水平地面上放有一质量为M的三棱柱体(倾角为q)，其上又放一质量为m的小三棱柱体。它们的横截面都是直角三角形，M的水平直角边的边长为a，m的水平直角边的边长为b。两者的接触面亦为光滑。设它们由静止开始滑动

求：当m的下边缘滑到水平面时，M在水平面上移动的距离。

解：对M 与m 组成的系统，水平方向动量守恒。设M与m相对地面的速度分别是V 和v，m相对于M的速度为v’，则

由相对运动公式

将(2)式代入(1)式得：

设m的下边缘滑到水平面需用的时间为t ，将上式

两边对时间积分，有:

显然，= S 就是M相对水平地面移动的距离。

而 是m相对于M在水平方向移动的距离。

最后求得M在水平面上移动的距离：