二 绕定轴转动的转动定理的应用
刚体转动定律的应用与平动问题中牛顿定律的应用的完全相似。
主要类型有：
A.已知刚体所受力力矩求刚体转动状态。
B.已知刚体转动状态求刚体所受力矩。
C.已知刚体部分转动状态和部分力矩求解未知力矩和未知转动状态。
刚体转动定律应用的解题步骤
A.确定研究对象，分析刚体所受力、力矩。
B.建立坐标系，列转动动力学方程以及必要的平动动力学方程。
C.解算及讨论。
例：电风扇开启电源时，经t1时间达到额定转速w0，关闭电源时经时间t2停止。设电风扇的转动惯量为I，且电机的电磁力矩与摩擦力矩为恒量。
求：电机的电磁力矩
解：设电风扇的电磁力矩、摩擦力矩分别为M、Mf
电风扇开启时受电磁力矩与摩擦力矩的作用，即：
当电风扇达到额定转速时： 
电风扇关闭过程中，只受到摩擦力矩的作用，即：
达到停止时： 
解此联立方程组，得： 
例：质量为M、半径为R的匀质柱体可绕通过其中心轴线的光滑水平固定轴转动；柱体边缘绕有一根不能伸长的细绳，绳子下端挂一质量为m的物体，如图所示。
求：柱体的角加速度及绳中的张力。
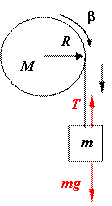
解：对柱体： 
错误！
正确的解法是用隔离体法
对m：
对柱：
解得：
， 
例：质量m1=24kgm2=5kg的具有水平光滑轴的圆盘形定滑轮后挂有m=10kg的物体。
求：物体m由静止开始下落h=0.5m时，物体的速度及 绳的张力。
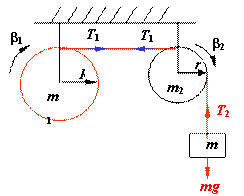
解：各物体受力情况如图所示
求解联立方程，代入数据，可得：
例：一根质量为m、长为l的均匀细棒AB，可绕一水平光滑轴o在竖直平面内转动，o轴离A端的距离为 l/3。今使棒从静止开始由水平位置绕o轴转动。
求：棒转过角q时的角加速度和角速度。
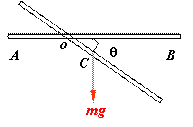
解：各物体受力情况如图所示。
又因 
所以 
完成积分得 
讨论:
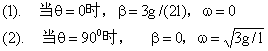
例：一质量为m、半径为R的匀质圆盘绕通过盘心且垂直于盘面的光滑轴正以wo的角速度转动。现将盘置于粗糙的水平桌面上，圆盘与桌面间的摩擦系数为µ
求：圆盘经多少时间、转几圈将停下来？
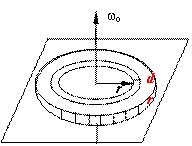
解：摩擦力分布在整个盘面上，计算摩擦力的力矩时，应将圆盘分为无限多个半径为r、宽为dr 的圆环积分。故摩擦力矩：
转动惯量：
于是得：
又由
，所以停下来前转过的圈数为