§9-2　电场能量及环量函数

一　电场力能的性质

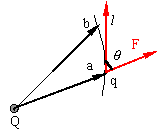
1.电场力作功的特点、电势能、电势

作为特例，我们首先研究点电荷的能的性质：

　　　　　

其中，定义：，称为点电荷的电势能。

讨论：A.点电荷的电场力为保守力：，

　B.点电荷的电势能：

注意积分方向，在电势能定义中，电量Q有正负之分。

C.点电荷电势:(电势反映电场自身能的性质)

　D.点电荷的电势差：

推广：考虑到任意电荷分布产生的电场都可以看作为点电荷产生的电场的叠加，因此上述关于点电荷的结论可以推广到任意静电场情形。

结论：A.静止电荷产生的电场是保守力场。对应的电场是保守场

， ； ，

B.静电场中都可以引入电势能：　　　

C.静电场的电势:　　　　　　　　　(电势反映电场自身能的性质)

D.静电场的电势差：　　　　　　　　(注意积分的方向)

2.电势的求解方法

1.离散体电势的求解:　对离散体的电荷体系，由电场的叠加原理可以求解

例：给出任意离散体的电势通用求解方法

解：选择无限远处的电势为零，由电场的叠加原理，有：

　

结论：离散体系在空间某点产生的电势，等于各单元在该点产生的电势的代数和。

例：电偶极子在空间的电势分布

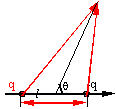
解：由点电荷的电势计算公式及电势的叠加原理：

　　　　

当：r>>l时，，，

当：时，，电偶极子轴线上电势始终为零。

当：时，。当：时，

2.连续体电势的求解方法

例：给出求解任意连续体空间电势的方法

解：方法一：叠加方法：

选择无限远电势为零点。将连续体在空间某点的电势看作为连续体内部若干点电荷在该点独自产生的电势的叠加，由点电荷电势计算公式及电势的叠加原理，就可求解：

因此，只要能将电量微元与空间坐标联系起来，对电量的积分，就变成在存在电荷分布区域内对空间坐标的积分，问题就转化为空间的积分运算了。

例：连续体分布：

在直角坐标系中：

在球坐标系中：

连续面分布：直角坐标　

　　极坐标：　　　　　

z

连续线分布：

直角坐标　

方法二：定义求解方法

x

　　由定义：，首先求出电场强度，再由定义式沿任意路径从待求点积分到无限远。由于电场力为保守力，从待求点向无限远积分与积分路径的选择无关，因而可以依求解的方便性选择积分路径。

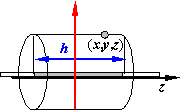
例：求线电荷密度为l，均匀电荷分布、长l的导线的电势分布

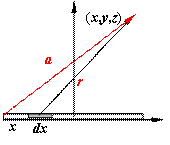
解：叠加方法

如图，取微元，设导线长度为l，由对称性，可取待求点的坐标为(x,0,z)

讨论：当l为无限长时，是否可以由上述答案令来得到呢？

(1).令：

(2). 当l为无限长时，用高斯定理求解出电场强度矢量，再

由定义方法求解。

　　由高斯定理：

按定义方法：

(3).仍然用定义方法求解，但选取有限远点为零势能点，由上述方法(2)：

　

(1)、(2)的结果对比较有限远点的电势大小是没有意义的。只有(3)的结果可以比较有限远点的电势大小。其原因是对无限长、无限大带电体的电势分布，不能选取无限远点为零势能点。(因为，选择无限远点为零势能点，由对称性，待求点相对于别的电荷而言，也是无限远点)

结论：一般地，对无限长、无限大电荷分布，不能选取无限远点作势能零点；通常也不能选择电荷所在点为势能零点。

一般地，当电荷分布为无限长、无限大，或电荷分布具有简单的几何对称性时，用高斯定理求解出电场强度，然后用定义方法求解电势，是比较简单的方法。

　　一般地，当电荷分布不具有对称性时，应用叠加方法求解电势是比较简单的方法。

例：半径分别为R₁、R₂两均匀、同心带电球壳，电量分别为q₁、q₂，求空间电势分布。

解：方法一：定义方法

由于题目电荷分布具有球对称性，因而，用定义方法求解是比较方便的。

首先，由高斯定理求出电场分布：

当：时，E=0；当R₁<r<R₂时，；当r>R₂时，

然后，由定义式求出电势分布：

　　　当时

　　　　　　　　当R₁<r<R₂时

　　　　　　　　　　　　　　 当r>R₂时

电势差：　　　　　　　

方法二：叠加方法求解

首先求出每个单元的电势分布：

对q₁： 　当r>R₁；　　　　　　　当时

对q₂： 　当r>R₂；　　　　　　　当时

然后，对各区域电势叠加，可以得到与方法一相同的结果（略）。

讨论：本题容易出错的地方在于误认为E=0的地方U=0。容易考虑掉球面内部的电势。事实上，对每一个球面，虽然球面电荷对其内部电场强度没有贡献，但对电势有贡献。

例：一均匀带电细杆, 长为l=15.0cm, 线电荷密度l=2.0´ 10^-7c/m

求: (1) 细杆延长线上与杆的一端相距a=5.0cm处的电势

(2) 细杆中垂线上与细杆相距b=5.0cm处的电势

解：(1)建立图示坐标系, 由电势叠加原理, 可得所给点的电势：

=

(2)中垂线上一点的电势为:

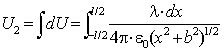
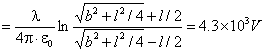
例：1)求均匀带电圆环轴线上一点的电势(电量q半径R) 2)轴线上a，b两点，，， 一带电量为Q的粒子从a点运动到b点. 求在此过程中静电力所作的功

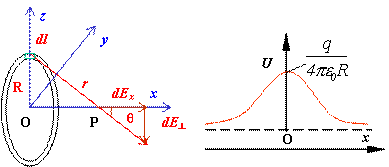
解：1)

环心： x=0

（2）a点

b点

例：设球面半径为R，总带电量为Q,, 见图

求：均匀带电球面的电场中的电势分布。

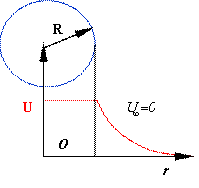
解：

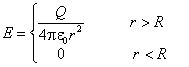
在球面处场强不连续，而电势连续

例：两同心的均匀带电球面，半径分别R₁=5.0cm, R₂=20.0cm,已知内球面的电势为U₁=60v, 外球面的电势 U₂=-30v

求: (1)内、 外球面上所带电量

　　(2) 在两个球面之间何处的电势为零

解：(1)以q₁和q₂分别表示内外球所带电量.

由电势叠加原理

(2) 由设距球心为r处的P点电势为零

由此可得

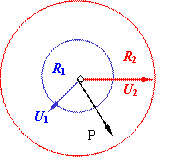
例：求无限长均匀带电直线的电场中的电势分布

解:已知场强为：方向垂直于带电直线。若仍然选取

　 无穷远为电势零点，则由积分可知各点电势将为无限大而失

　 去意义。此时，我们可以选取某一距带电直导线为r_B的B点

　 为电势零点，则距带电直线为r的p点的电势：

强调：当电荷分布扩展到无穷远时，电势零点不能选无穷远处

例：半径为R的均匀带电球面, 带电量为q,沿矢径方向上有一均匀带电细线,电荷线密度为l, 长度为 l,细线近端离球心距离为r₀.

设球和线上的电荷分布不受相互影响.

求：细线所受球面电荷的电场力和细线在该电场中的电势能.(设无穷远处的电势为零.)

　

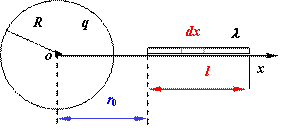
解: 建立图示坐标系， 在x处取线元dx, 其上电量为dQ=ldx,

　 该线元在带电球面的电场中所受电场力为:

整个细线所受电场为方向沿x轴正方向.

电荷元在球面电荷电场中具有电势能为

整个线电荷在电场中具有电势能为:

例：求电偶极子在均匀外电场中的静电势能：

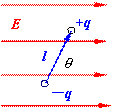
解:

上式表明：电偶极子取向与外电场一致时，电势能最低；取向相反时, 电势能最高。

电子在原子核的电场中的电势能：

上式以无限远为电势的零点。