二　电场强度与电势的关系

1.相关概念

　等势面：a.由电势相等的面构成的曲面。b.相邻等势面间的电势差相等

2.电场强度与电势的关系

数学预备知识。方向导数：　

　　　　　　　 取极限，得：

梯度及其方向：　

对任意曲面：F[x(t),y(t),z(t)]=0，坐标是t的参数方程。曲面在t₀点的切线的方向矢量为：

由全导数的计算公式：

或：　，因此，曲面方程的梯度方向是曲面的法向方向。

(1).电场强度与电势的关系

A.积分关系：　　　B.微分关系：

微分关系的推导：考察电势沿任意方向的变化率，由方向导数的定义：

　

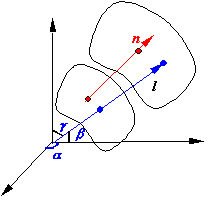
其中：cosa、cosb、cosg为方向余弦。

显然：

　　　　　　　　　　　　　　　

定义标量场的梯度：

于是：

讨论：等势面与电场间的关系：

a.电场力沿电力线方向对电荷作正功，电势能降低，于是：

分量式：，，

考虑到——曲面方程的梯度方向是曲面的法向方向。于是有下面结论成立：

等势面与电力线处处正交，且电力线的方向总是指向电势降低的方向。并是电势降低最快的方向

结论1：电场强度等于电势的负梯度;等势面分布较密的地方，电场强度愈大；电荷沿等势面移动时，电场力不作功；电场强度与电势的梯度相关，而与电势本身没有直接关系。

(2).利用电势求解电场强度

　首先求解静电场的电势，然后利用结论1求解电场强度。这是一种重要而常见的方法。

说明：在利用电势求解电场强度时，可以通过判断电场的对称性从而不一定要对电势每一个分量求偏导数。