二　电介质中的库仑定理与高斯定理

1.电介质中的库仑定理——实验定律：　　

　　　

　其中：，称为相对介电常数。相对是指相对于真空的介电常数。。

2.电介质的电场强度矢量——实验定律

　　　　

对点电荷：

电介质中的静电作用力或电场强度比真空中对应的静电作用力或电场强度小，是因为电介质极化造成的。

例如，一个正电荷处于无限大的电介质中，其周围必然产生负的极化电荷。那么，在介质中任意一点的电场强度等于原点电荷与极化电荷共同产生的电场强度，其值一定比在真空中产生的场强小。

3.电介质中的高斯定理

讨论电介质中高斯定理的思路：将电介质中的电量考虑为原自由电荷和自由电荷激发的束缚点电荷的代数和，对应地，介质中的电场强度或电通量就成为两种电荷的总贡献。这样，就把电介质中的电场强度或电通量问题转化为讨论真空中的对应问题了。这一思路包含两个逻辑步骤：

A.定量讨论电介质中自由电荷产生的束缚电荷问题。　　B.将电介质问题转化为真空电场强度分布或电通量问题

A.关于束缚电荷的定量讨论

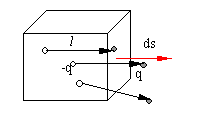
a.束缚体电荷分布

　　如图，在介质中取一长方体微元，长方体微元的高很小。

定义电介质极化电荷的体密度：电介质极化电荷的体密度等于

　　单位体积内极化电荷的电量。

长方体微元内通过图示表面的极化电荷电量：

其中：n表示单位体积内的分子数(电偶极矩数)，表示一个电偶极子的电偶极矩，，表示电偶极子电荷间的间距(只有距微元表面为l的偶极子才对体极化电荷密度有贡献)。

长方体微元内的总极化电荷为：　　而　

即：　　　

在上式中，用到了曲面积分与体积分的奥－高公式。

结论1：介质中极化电荷的体分布为：

体积微元的极化电荷总量为：

b.束缚面电荷分布

如图，在两种介质交界面的薄层内，存在极化电荷，介质1对薄层的极化电荷电量贡献为：

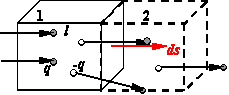
介质2对薄层的极化电荷电量贡献：

这里，考虑了留在薄层内极化电荷的正负。

薄层内的极化电荷电量总量：

其中，表示面极化电荷密度，为1®2的面积微元的法向。

结论2：在两种介质的交界面上的极化面电荷密度：

或交界面的薄层内的总极化电荷为：

B.介质中的高斯定理

如上所述，介质中的电场强度等效于在真空中同时考虑极化电荷和自由电荷产生的场强。于是，由真空中的高斯定理：，可得到介质中的高斯定理：

　　因　　　同时，令　

　　　　　　

定义电位移矢量：　　　　　　　　　

介质中的高斯定理：　　　　　　　　

讨论：A.关于介质中的高斯定理

　　介质中的高斯定理右边，只含自由电荷电量的代数和，不包含极化电荷的电量。极化电荷电量已经考虑在电位移矢量中。且等式右边不包含任何介电常数。

与真空中的高斯定理类似，电介质中的高斯定理只是电位移矢量通量与电量的关系，不直接反映电位移矢量与电量的关系。

高斯定理左边的电位移矢量是高斯面内、外自由电荷和极化电荷产生的矢量和，而不只是高斯面内的自由电荷、极化电荷产生的电位移矢量。

B.关于电位移矢量

电位移矢量没有明确的物理意义，只是一个中间代换量，它使介质中的高斯定理形式简洁。同时，电位移矢量也可以用电位移矢量力线加以形象表述，但不一定与电力线方向一致。

电位移矢量与由自由电荷产生的电场强度、极化强度有关，但其通量函数只与自由电荷电量有关。

C.关于极化强度

在教材中，极化强度矢量必须由实验确定，它与介质性质有关，对于各向同性的均匀介质，有极化强度的实验定律：，称电介质的极化率。

于是：　

几个重要关系：，，，，

4.介质中高斯定理的应用

应用介质中的高斯定理求解问题与应用真空中的高斯定理求解问题类似，关键还是判断带电体系的对称性，并正确选取高斯面。(希望学生自己对比研究)。

说明：如果系统有多种介质，那么，选取的高斯面处于什么介质，电位移矢量中的介电常数就带这种介质的介电常数(考察问题1)。

求束缚面电荷，一般先由求解束缚面电荷密度，再求解束缚面电荷。对于金属或真空，极化强度矢量为0。极化强度矢量由计算。

例：一个金属球半径为R，带电量 q₀ ，放在均匀的介电常数为e 电介质中。

求：任一点场强及界面处s=?

解：导体内场强为零。由球对称性

因为

注意到:

上例也说明当均匀电介质充满电场的全部空间时，或当均匀电介质的表面正好是等势面时，有：