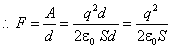§9-6 电场的能量及能量密度
一电场的能量及能量密度
1.电场的能量
由上述讨论可知,电场的能量,实际可以看成是电容器中储存的能量。即:
![]()
(希望大家仔细思考求解电场能量的思路,这是很巧妙且很有有意义的)
2.电场的能量密度
能量密度:电场中单位体积的能量,称为电场的能量密度。
推导思路:考虑到任意情况下推导电场的能量密度相对要困难一些[1],我们这里从平行板电容器的特例出发,推得平行板电容器的能量密度,然后作推广,并认为所得结论对任意电场能量密度均适用。
因 ![]() ,对平行板电容器,有:
,对平行板电容器,有:![]() ,
,![]()
于是:![]()
单位体积内的能量——能量密度为:![]()
推广:对任意静电场,假定上述结论均成立,可以得到结论:
静电场的能量密度:![]()
静电场的能量:![]()
讨论:A.适用条件:静电场,均匀介质
B.求解电场的总能量,或某一体积内静电场的总能量,总是通过能量密度积分得到。积分区域应是静电场分布的区域,或待求的体积区域。
例:求解球形电容器储存的静电能量

解:设球形电容器的内、外半径分别为R1、R2,内外球面带电量分别为Q、
-Q,两球面中介质的介电常数为e。显然,只有两球面之间有静电场分布。
如图取高斯面: ![]()
静电场的能量密度:![]()
静电场的总能量: ![]()
![]()
说明:用能量密度求解静电场的能量,首先将电场分量表述为空间坐标的函数,然后对静电场分布区域积分。其中,关键是正确确定积分区域。
例:均匀带电球体,半径为R,体电荷密度为r,求:此带电球体系统的静电能。
解:由高斯定理![]()
![]()
![]()
![]()
![]()
同理 ![]()
![]()
![]()
![]()
![]()
![]()
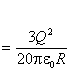
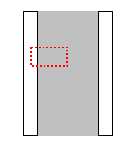
例:一平行板空气电容器的板极面积为S,间距为d,用电源充
电后两极板上带电分别为±q。断开电源后再把两极板的距离拉开到2d。
求:(1)外力克服两极板相互吸引力所作的功
(2)两极板之间的相互吸引力。(空气的电容率取为e0)

解:
(1)两极板的间距为d和2d时,平行板电容器的电容分别为
![]()
板极上带电±q时所储的电能为: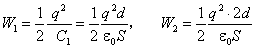
故两极板的间距拉开到2d后电容器中电场能量的增量为 ![]()
根据功能原理可知,外力的功等于系统能量的增量![]()
(2)设两极板之间的相互吸引力为F ,拉开两极板时所加外力应等于F ,所以外力反抗极板间的电场力作功A=Fd