第十三章 光 的 干 涉
思考题参考答案
s13-1答：由n1<n2， n2>n3可知，光线在薄膜上下两表面反射时有半波损失，故选(B)。
s13-2答：光程差=光程S2P-光程S1P，故选（B）。
s13-3 答：普通的独立光源是非相干光源。选（D）。
s13-4 答：光程就是在相同的时间内光在真空中走过的路程，选（C）。
s13-5答：由条纹间距公式
，
s13-6答：不同频率(颜色)的光是不相干的，故选（D）。
s13-7答：由于光经反射镜M反射后有半波损失，明暗纹位置对调，故选（C）。
s13-8答：明条纹和暗条纹光程差
，故选(B)。
s13-9答：
反射加强，最小厚度k=1，得
，选（B）。
s13-10答：由
，q
增大，条纹间隔l变小，并向棱边方向平移。选（A）。
s13-11答：由
，对第5条暗纹， k=4，
，故选（A）。
s13-12
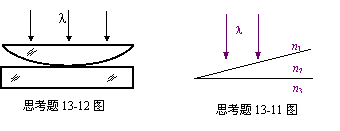
答：等后处内移，条纹向中心收缩。选(B)。
s13-13答：由
，明纹；
，暗纹；
左边：无半波损失，半=0；e=0处为明纹。
右边：有半波损失，半=；e=0处为暗纹。故选（C）。
S13-14答：由2(n-1)e=l，得e=λ/[2(n-1)]，故选（D）。
习题参考答案
x13-1
解
由加强条件 
kl
已知d=
得 kl=
40000nm
当 ……k=5 ，
l=800nm
k=6 ， l=666.7nm
k=7 ， l=571.4nm
k=8 ， l=500nm
k=9 ， l=444.4nm
k=10 ，l=400nm
以上六种波长的光在所给的观察点得到最大限度地加强。
x13-2纹所在处o变为第五级明纹。设入射单色光波长λ=4800Å，求玻璃片的厚度d(可认为光线垂直穿过玻璃片)。
解
覆盖缝玻璃片后，原中央明条纹所在处o变为第五级明纹，表明此时从S1和S2发
出的光线到达o点的光程差为5λ。根据光程的概念，有
d=（n2- n1）d =5l
得
x13-3解 (1) 设零级明纹中心移到P点处，P点到o点的距离为x，则
l1+ r1=l2+ r2
由于 r2- r1=dx/D，
l1-l2=3λ
于是零级明纹到屏幕中央
o点的距离
x=3Dλ/d
(2) 明纹条件
d= dx/D-3λ= kl
xk=(kl+3λ)D/d
相邻明纹间距为
xk+1 - xk=Dλ/d
x13-4解 光在一氧化硅薄膜上下表面的反射无半波损失，故由薄膜公式有
d反=2en2=kl
对应于最小镀膜厚度，k=1，由此得
=1400Å=1.4×10
x13-5解 (1) 由于不存在半波损失，反射光中又只有420nm的紫光和630nm的红光得到加强，故有
2en2=kl1， l1=420nm
2en2=(k-1)l2， l2=630nm
由此得
k´420nm=(k-1)´630nm
k=3
二氧化硅(SiO2)薄膜的厚度为
=420nm =4.2×10
(2) 干涉相消条件为
2en2=
=
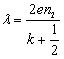在白光(400nm¾760nm)范围内，只有k=2，得
=504nm
也就是说，反射光中只有504nm的光因干涉而相消。
(3) 在与薄膜法线成30º角的方向上观察，反射光加强的条件为
=
在白光(400nm¾760nm)范围内，也只有k=2，得
=594nm
也就是说，在与薄膜法线成30º角的方向上观察，反射光中只有594nm的黄光加强了。
x13-6解 光在油膜上下表面的反射无半波损失，故由薄膜公式有
d反=2en2=(k+
)l
当l1=500nm时，有
2en2=(k1+)l1
(1)
当l2=700nm时，有
2en2=(k2+)l2
(2)
由于500nm和700nm这两个波长之间无别的波长发生相消，故k1、 k2为两个连续整数，且k1> k2，所以
k1= k2+1
(3)
由式(1) (2) (3)解得：
k1=3，
k2=2
可由式(1)求得油膜的厚度为
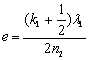=6731Å=6.731×10
x13-7解 有气体时，由薄膜公式有
抽去气体后，有
由以上两式求得这种气体的折射率
=1.00025
x13-8解 (1) 由薄膜公式，有
对第四条暗纹，k=3，有
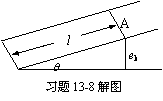所以A处膜厚： 
由于e4=lq
，l1=500nm，l=
=4.8×10-5rad
(2)当改用波长为l2=600nm的光时，有
d反=
所以此时A处是第3级明条纹。
(3)在第(2)问的情形，棱边处(e=0)为一暗纹，而A处是第3级明条纹，所以从棱边到A处的范围内共有3条明纹和3条暗纹。
x13-9解 (1) 由薄膜公式，有
求得
=2.32×10
(2) 由牛顿环的明环公式，第十个明环的半径为
=
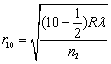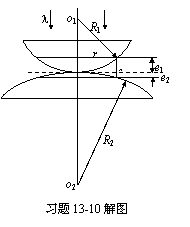
x13-10解 由薄膜公式，有
， 明纹，k=1,2,……
，暗纹,k=0,1,2,……
由本题解图，可知e=e1+e2，而
，
对明纹
明条纹半径：
，k=1,2,……
对暗纹
暗条纹半径： 
，k=0，1,2,……
x13-11解 (1) 由薄膜公式，有
当
k=0，eo=0 (油膜边缘处)
k=1，e1=2500Å
k=2，e2=5000Å
k=3，e3=7500Å
k=4，e3=10000Å
k=5，e5=12500Å>12000Å,略去。
由以上讨论可知，此时可看到5条明暗
相间的同心圆形条纹(对应k=0、1、2、3、4)。
(2) 当油膜继续扩展时，油膜半径扩大，
各处厚度不断减小，圆形条纹级数减少、间距增大。各处明暗交替出现，直至整个油膜呈现一片明亮区域。
x13-12解 (1)由公式
得
=6289Å
(2)插入一薄玻璃片后，迈克耳逊干涉仪两光路光程差的改变量为2(n-1)e；而每看见一条条纹移过，两光路的光程差应改变一个λ
，所以有
2(n-1)e=150λ
求得玻璃片的厚度
=5.9×10