第四章 振动学基础
参考答案
思考题
4-1答：物体运动时，如果离开平衡位置的位移（或者角位移）按余弦函数（或正弦函数）的规律随时间变化，这种运动就叫简谐运动。
也可从动力学角度来说明：凡是物体所受合外力（或合外力矩）与位移（或角位移）成正比而方向相反，则物体作简谐振动。
（1）不是简谐振动。从受力角度看，它受到地面的作用力，虽然是弹性力，但这外力只是作用一瞬间，而后就只在重力作用下运动。从运动规律来看，虽然是作往复运动，但位移时间关系并不是余弦（正弦）函数，而是作匀变速运动。
（2）是简谐振动。当小球在半径很大的光滑凹球面底部的小幅度摆动，若其角位移
，
，则其运动方程满足微分方程
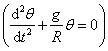，所以是简谐振动。
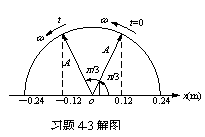
（3）作匀速圆周运动的质点在某一直径（取作x轴）上投影点对圆心o的位移随时间t变化规律遵从余弦函数，若设圆周半径为A，角速度为ω，以圆心为坐标原点，质点的矢径经过与x轴夹角为
的位置开始计时，则在任意时刻t，此矢径与x轴的夹角为
，而质点在x轴上的投影的坐标为
，这正与简谐振动的运动方程相同。可见，作匀速圆周运动的质点在直径上的投影点的运动是简谐振动。
质点作匀加速圆周运动，在直径上的投影x不是等周期性变化的，而是随着时间变化的越来越快，所以其投影点的运动不是谐振的。
4-2 答：在月球上，弹簧振子的振动周期不变，仍为
，但单摆的周期要改变，即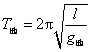
,
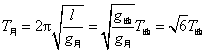
4-3答：相位是反映质点振动状态的物理量，其值为，一个弹簧振子正向最大位移开始运动时的相位为零；经过中点时的相位为
；达到负向最大位移时的相位为
；再回到中点向正向运动时的相位为
（或
）。
4-4答：（A）。
4-5答：（B）。
4-6答：（C）。
4-7答：（C）。
4-8答：（B）。
4-9答：（B）。
4-10答：（D）。
4-11答：（C）。
4-12答：（C）。
习题
4-1解：（1）
与振动方程的标准形式相比可知：
角频率 
;初周相
;振幅 
.
可求得 
最大速度 
最大加速度
(2)相位为
将
代入，则相位分别为
。
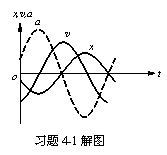
（3）该振动的
图，
图和
图如图所示。
4-2解：设弹簧的原长为l，悬挂m1后伸长
，则
, 
取下m1挂上m2后, 
时 
解得
或
应取
也可写成
振动的表达式为
4-3解：旋转矢量如图所示。由振动方程可得
， 
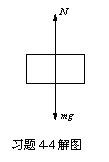
4-4解：（1）小物体受力如图所示。
设小物体随振动物体的加速度为a，
按牛顿第二定律有（取向下为正）
当
，即时
，小物体开始脱离振动物体，已知
系统的最大加速度为
，此值小于g，故小物体不会离开。
(2) 如使
，小物体能脱离振动物体，开始分离的位置由求得
即在平衡位置上方
，
可得
4-5解：因为
，所以，物体随板一起振动所需力为
此力由板对物的静摩擦力提供，此力的最大值为
物体在板上不发生滑动的条件是
，即
4-6解：钟摆周期的相对误差
等于钟的相对误差
，等效单摆的周期
设重力加速度g不变，则有 
令
，
并考虑到
，则有钟摆向上移动的距离
钟摆应向上移
4-7解：（1）由题意
， 
， 
（2）
， 
，
，
，
，
振动方程为 
4-8解：（1）
（2）当
时，
与
的合成
振幅最大为
当
时，与的合成振幅最小为
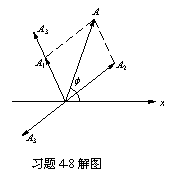
（3）用旋转矢量图表示（1），（2）两小题结果如图所示。
4-9解：如图所示，取x坐标，平衡位置为原点o，向下为正，m在平衡位置已伸长x0,
设m在位置x时有 
（因为弹簧伸长
）
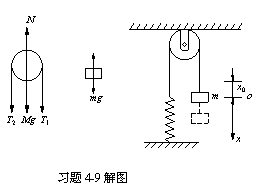由牛顿第二定律和转动定律列方程
联立解得 
由于x系数为一负常数，故物体作简谐振动，其角频率为
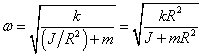
4-10解：如图（a）所示，设木块平衡时露出水平面的高度为a，浸入水中的深度为
。
（1）选水面上一点o为原点，向上为x轴
正方向，此时木块本身的重力等于水对木块
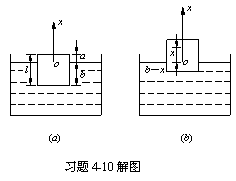的浮力，即 
（S为木块的截面积，
）。则有
，
当木块上移x，如图（b）所示，则木块
所受的浮力为:
。重力仍为
，合力为
，根据牛顿第二定律，有
，
将
代入上式得
令
， 得
，所以木块作简谐振动。
（2）木块的运动方程
时 
， 
由此得 
， 
（SI）