第五章 波动学基础
参考答案
思考题
5-1答：（B）。
5-2答：（C）。
5-3答：（B）。
5-4答：（A）。
5-5答：（C）。
5-6答：（A）。
5-7答：（A）。
5-8答：（D）。
5-9答：（C）。
5-10答：（B）。
5-11答：（C）。
5-12答：（D）。
5-13答：（C）。
5-14答：（A）。
5-15答：（C）。
5-16答：（B）。
习题
5-1解：
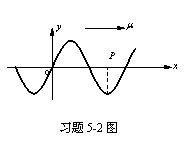
5-2解：（1）以o点为坐标原点。由图可知，初始条件为
,
所以
波动方程为 
（2）
的振动方程为
的振动方程为
（3） 
,
时
,时
5-3解：（1）由P点的运动方向，可判定该波向左传播。对原点o点处质点，时
,
所以
o处振动方程为 
波动方程为
(2)距o点
振动速度表达式是
5-4解：（1）坐标为x点的振动相位为
波动方程为 
（2）以B点为坐标原点，则坐标为x点的振动相位为
波动方程为 
5-5解：该波波速
，圆频率
，则
（1）任取一点P（见习题5-5解图①），
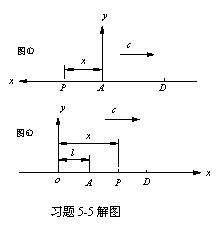可得波动方程为
将 
代入上式有
（2）任取一点P（见习题5-5解图②）
可得波动方程为
将
代入上式有
将
代入上式有
5-6解：
，又因
，所以
,
。题图中
，时，波形比题图中的波形倒退
，见习题5-6解图。
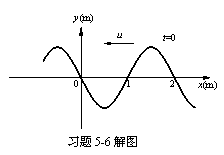此时o点位移
（过平衡位置）且朝y轴负方向运动，所以
5-7解：设o处振动方程为
，
当时，
,
所以
。
故入射波方程为 
在
处入射波引起的振动方程为
由于M是波密媒质反射面，所以处反射波振动有一个位相的突变。
反射波方程
合成波方程为
将P点坐标 
代入上述方程得P点的振动方程
5-8解：（1）由形成驻波的条件。可知待求波的频率和波长均与已知波相同，传播方向为x轴的负方向。又知
处待求波与已知波同相位，所以待求波的波动方程为
（2）驻波方程为 
即 
波节位置由下式求出：
离原点最近的四个波节的坐标为
5-9解：（1）o处观察者所接收到的拍音频率为声波直接传给观察者的声波频率
与经墙壁反射给观察者的声波频率
之差。
即拍频为 
(1)
按规定取S指向o坐标轴正方向，此时波源的速度
，观察者的速度
，于是
(2)
式中，
为声源静止时的频率，
反射壁不动，波源向反射壁运动，反射壁
相当于接受声波的观察者。故有
(3)
将式②，式③代入①得到
对上式整理后，得到
的二次方程为
利用求根公式，并只取正根，得到
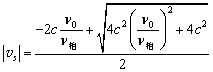
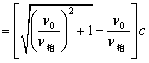
代入数值，求得
（2）若S不动，则S直接传给静止的观察者o的声波频率 
。
当反射面向o运动，亦即向S运动。取S指向反射面的方向为坐标轴正向，反射面相当于接受声波的观察者
，此时，
,
反射面接收到的频率
为
设反射面反射的声波被o处观察者接受到的频率为
，此时反射面可视为波源
，仍取指向o为坐标轴正方向。于是有
，代入公式有
拍频为
于是声源的频率为
