第二章 质点动力学

知识点：

1． 牛顿定律

第一定律：任何物体都保持静止的或沿一直线作匀速运动的状态，直到作用在它上面的力迫使它改变这种状态为止。

第二定律：运动的变化与所加的动力成正比，并且发生在这力所沿的直线方向上。即，

当质量m为常量时，有

在直角坐标系中有 ， ，

对于平面曲线运动有 ，

第三定律：对于每一个作用总有一个相等的反作用与之相反，或者说，两个物体之间对各自对方的相互作用总是相等的，而且指向相反的方向。即

2． 非惯性系与惯性力

质量为m的物体，在平动加速度为a₀的参照系中受的惯性力为

在转动角速度为w的参照系中，惯性力为

3. 功

质点在力F的作用下有微小的位移dr，则力作的元功定义为

对质点在力作用下的有限运动，力作的功为

在直角坐标系中，此功可写为

应当注意，功的计算不仅与参考系的选择有关，一般还与物体的运动路径有关。只有保守力(重力、弹性力、万有引力)的功才只与始末位置有关，而与路径形状无关。

4. 动能定理

质点动能定理：合外力对质点作的功等于质点动能的增量。

质点系动能定理：系统外力的功与内力的功之和等于系统总动能的增量。

应当注意，动能定理中的功只能在惯性系中计算。

5. 势能

重力势能： E_P=±mgh，零势面的选择视方便而定。

弹性势能： ，规定弹簧无形变时的势能为零，它总取正值。

万有引力势能： ，取无穷远处为零势点，它总取负值。

6. 功能原理

即：外力的功与非保守内力的功之和等于系统机械能的增量。

7. 机械能守恒定律

外力的功与非保守内力的功之和等于零时，系统的机械能保持不变。即

8. 动量定理

合外力的冲量等于质点（或质点系）动量的增量。其数学表达式为

对质点

对质点系

在直角坐标系中有

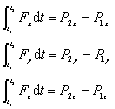
9. 动量守恒定律

当一个质点系所受合外力为零时，这一质点系的总动量矢量就保持不变。即

当时，常矢量

在直角坐标系中的分量式为

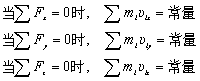
10. 角动量定理

质点的角动量：对某一固定点有

角动量定理：质点所受的合外力矩等于它的角动量对时间的变化率

11. 角动量守恒定律

若对某一固定点而言，质点受的合外力矩为零，则质点的角动量保持不变。即

重点：

1. 深入理解牛顿三定律的基本内容。

2. 掌握应用牛顿定律解题的基本思路，能用微积分方法求解一维变力作用下的质点动力学问题。

3. 初步掌握在非惯性系中求解力学问题的方法；理解惯性力的物理意义，并能用以解决简单的力学问题。

4. 熟练掌握功的定义及变力作功的计算方法。

5. 理解保守力作功的特点及势能的概念。

6. 掌握动能定理及功能原理，并能用它们分析、解决质点在平面内运动时的力学问题。

7. 掌握机械能守恒的条件及运用守恒定律分析、求解综和问题的思想和方法。

8. 掌握动量定理。学会计算变力的冲量，并能灵活应用该定理分析、解决质点在平面内运动时的力学问题。

9. 掌握动量守恒定律。掌握系统动量守恒的条件以及运用该定律分析问题的思想和方法，能分析系统在平面内运动的力学问题。

10. 掌握质点的角动量的物理意义，能用角动量定理计算问题。

11. 掌握角动量守恒定律的条件以及运用该定律求解问题的基本方法。

难点：

1． 变力作用下的质点运动问题。

2. 非惯性系中应用惯性力求解质点力学问题。

3. 计算变力的功。

4. 理解一对内力的功。

5. 机械能守恒的条件及运用守恒定律分析、求解综和问题的思想和方法。

6. 计算变力的冲量。

7. 用动量定理、动量守恒分析、解决质点二维运动时的力学问题。

8. 角动量、力矩的矢量性。

9. 正确运用角动量定理及角动量守恒定律求解问题。