1.量子力学中与力学量有关的基本假设有哪些？

 关于力学量及其表示，量子力学有三条基本假定：

(1)有关量子体系运动的每一个力学量都可以用一个线性厄密算符 来表示．

(2)对于该力学量的测量值，必定是相应的线性厄米算符 的本征值 之一．

(3)如果体系处于 态，该态可按算符 的本征态 展开

那么在态 中，测量力学量 取值 的概率正比于展开系数 的模的平方 ．

以上三条假定，共同给出了关于力学量的完整概念．

可见，在量子力学中，力学量与态是相对独立的概念。而力学量算待与其数值也有不同含义．在经典物理中，力学量可由运动状态完全确定，不必引入算符表示．并且，力学量与其数值也是一体的概念．

2. 量子力学为什么要用算符表示力学量 ?

 用算符表示力学量，是由于量子体系所固有的波粒二象性所要求的．这正是量子力学处理方法上的基本特点之一．我们知道，表示量子态的波函数是一种概率波．因此，即使在确定的量子态中，也并非各种力学量都有完全确定区而是一般地表现为不同数值的统计分布．这就注定了经典力学量的表示方法 (可由运动状态完全决定)不再适用，因此需要寻求新的表示方法．
我们从力学量平均值的表示式出发，来说明引入算符的必要性．如果体系处于态 中，则它的位置平均值为

类似地，它的动量平均位也可表示为

但是要求出第二个积分，必须将 表示为 的函数．然而这是办不到的．因为按不确定关系 的表示是无意义的，因此不能直接在坐标表象中按上式求动量平均值．我们可先在动量表象中求出动量平均值，再转换到坐标表象中去．

利用 有

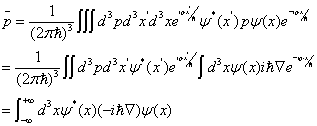
可见，若在坐标表象中计算动量平均值，那么动量矢量恰与算符 相当，实际上，任何一个力学量在自身表象(连续谱)中计算其平均值，都与一个特定的算符相当，这就自然地引入了算符表示的概念．

用算符表示力学量的问题还可以从另一角度来说明．我们知道量子力学中，力学与力学量之间的关系，从其数值是否能同时确定来考虑，有相互对易与不对易两种，而经典力学量之间都是对易的，因此经典力学量的表示方法不能适用于量子力学．然而在数学中，算符与算符之间一般并不满足交换律．也就是存在不对易的情形．因此用算符表示力学量是适当的．

3.什么是算符的本征值和本征函数？它们有什么物理意义？

 含有算符 的方程

称为 的本征值方程, 为 的一个本征值，而 则称为 的属于本征值 的本征函数．

如果算符 代表一个力学量，上述概念物理意义如下：

当体系处于 的本征态 时，测量 的数值是确定的，恒等于 ，并且根据本章开头列出的假设，当体系处于任意态时，单次测量 的值必等于它的诸本征值之一．

4.什么是算符的期望值(平均值)？它们有什么物理意义？

 力学量 的平均值(或称期望值)的一般定义为

它的意义包括以下几点：
(1)当体系处于 态时， 就等于对于 的所有测量值的平均；
(2)如 为 的一个本征态，则 就等于对应的本征值；
(3)如果可在经典力学与量子力学间建立对应关系，那么与经典力学量对应的便是量子力学中的力学量的平均值。

5. 厄米算符有哪些特特性？

 厄米算符具有如下特性．
(1) 厄米算符的本征值为实数；
(2) 厄米算符在任何态中的平均值亦为实数；
(3) 厄米算符属于不同本征值的本征函数彼此正交；
(4) 描写力学量的厄米算符的本征函数系是完全系．

6.为什么作为力学量必须要求算符是线性的、厄米的？

 力学量必须为线性算符．这是由量子态叠加原理所要求的．
真实力学量的任何测虽值当然必须是实数，因此它的本征值必为实数，这就决定了力学量必须由厄米算符来表达

7.设算符 ， 不对易，[ , ]= ,但是 和 及 对易，即[ , ]=0,[ , ]=0,试计算：

[ ， ]，[ ， ]，[ ， ]，[ ， ]，其中 为正整数， 为参变数， 为任何可以展开成正幂级数的函数。

 解： 在一下的计算中，略去算符记号“ ^”，

将 换成 就有

代入上式，即得

重复这种递推过程，即得

（1）
根据定义，

因此

令 ，即得

（2）

如令 ，则 ，式（2）中作此置换，即得

（3）

设

利用式（ 1），即得

（4）

其中

式（ 2）和（3）均可视为式（4）的特例

8．设算符 和 不对易， ，但是 和 及 对易，即 ， 。

试证明Glauber公式：

 证明： 引入参变数 ，作

（1）

注意 。上式对 求导，得到

（2）

而根据第 7题式（3）

（3）

代入式（ 2），即得

（4）

以 乘之，得到

（4'）

积分，即得

因此

由于 ，故得

（5）

以 乘上式，即得

（6）

如令 ， ，则 上式变成

（6'）

式（ 6）和（6'）中取 ，即得