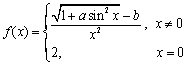2004级(上)期末试题(A)

一、（12分）求极限:

1. 。                  2.

二、（12分）:

1. 设 在 处连续，试确定a, b的值.

2. 设 在 点处有 ，而 点及其邻域有定义且有界，试证明函数 在 点处可导，并求 .

三、（12分）

1. 设 由方程 确定，求 。

2. 设曲线方程为 ，求此曲线在x=2点处的切线方程。

四、（12分）求不定积分:

1. 2.

五、（12分）计算定积分:

1. 2.

六、（8分）A、B两厂在直河岸的同侧，A沿河岸，B离岸4公里，A与B相距5公里，今在河岸边建一水厂 ，从水厂到B厂的每公里水管材料费是A厂的 倍，问水厂 设在离A厂多远处才使两厂所耗总的水管材料费为最省？

七、（9分）已知可导函数 满足 ，求 。

八、（9分）设 由 所围成的平面图形.

(1)  求平面图形 的面积;

(2)  求平面图形 绕 轴旋转所成的立体的体积。

九、（8分）证明：当 时， 。

十、（6分）设 上连续，在(0, 1)内可导，且 ，证明：存在一点 ，使得