2006级（上）期末试题(B)

一、填空题（10分，每小题2分，每人只选做5个题，不得多做）

1. . .

2 用 语言叙述数列 以 为极限的定义 . .

3. 设 , 则 .,.

4. 设 ，则 .

5．函数 的下上凸区间是 , 上凸区间是 .

6．定积分 .

二、选择题（15分，每小题3分, 每人只选做5个题，不得多做）

1. 设 则当 时, 是 的 ( ) .

（A）高阶无穷小； （B）低阶无穷小；

（C）等价无穷小； （D）同阶无穷小但不等价.

2. 数集 的所有聚点的集合是（ ）.

（A） 三点组成的集合； （B）开区间 内所有点的集合；

（C）闭区间[ ，1]]上所有点的集合； （D）空集.

3. 函数 的跳跃间断点是 ( ).

（A） ； （B） ；

（C） ； （D）.不存在.

4．设函数 , 则 在 处 ( D ).

（A）极限不存在; （B）极限存在但不连续;

（C）连续但不可导; （D）可导.

5. 函数 的 阶麦克劳林公式中， 项的系数是( ).

（A） ； （B） ； （C） ； （D） .

6. 设 则 ( ).

（A） 0； （B） ； （C） ； （D） .

三、求极限（12分，每小题6分）

1. 2.

四、求积分（12分，每小题6分）

1． ； 2. ..

五、（12分，每小题6分）

1．计算 ；

2. 求微分方程 满足条件 的解.

六、（8分）设函数 由方程 所确定，试求 .

七、（8分）根据 的取值范围，讨论方程 在 上有几个实根？

八、（11分）设曲线 与曲线 在点 处有公共切线，求：

( 1 ) 常数 及切点 ； ( 2 ) 两曲线与 轴围成的平面图形 的面积；

( 3 ) 平面图形 绕 轴旋转而成的旋转体的体积.

九、（6分）注意：以下两题选做一题，不得两题都做

(1) 设函数 在 上连续，在 内可导，

求证： 使得

(2) 利用确界存在定理证明：单调增加有上界的数列必定收敛.

十、（6分）设 在 上的导数连续，

求证：
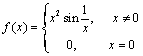