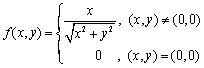2006级(下)期末试题B

一、填空题（每题3分，合计１5分）

1. 设 ，则 .

2、函数 在点 处指向点（2, 0）方向的方向导数等于 .

3、将二次积分 化为极坐标下的二次积分 .

4、设曲线L为沿 从点 的弧段，则曲线积分 .

5、设f(x)以2为周期，它在 上的表达式为 ，则 的傅里叶级数在 上的和函数表达式 .

二、单项选择题（以下6个题只选做5个题，每题3分，合计１5分）.

1、 的任意点集的全部边界点所组成的集合 ( ) （供H班学生选做）

（A）是开集；（B）是闭集；（C）既是开集又是闭集；（D）两者都不是 .

2. 设 不连续，则 处（ ）

（A）偏导数必不存在； （B）必不可微；

（C）至少有一个方向的方向导数不存在； （D）以上都不对.

3、设 ，则 的偏导数（ ）

（A） （B）

（C） （D

4、非齐次线性微分方程 的特解形式为（ ）

（A） （B） （C） （D .

5、设S为曲面 外侧，则曲面积分 （ ）

（A）0； （B） ； （C） ； （D） .

6、设 ，则下列级数中肯定收敛的是（ ）

（A） ； （B） ； （C） ； （D） .

三、（8分）设方程 确定函数 ，其中F可微，求

四、（8分）求曲线 上平行于平面 的切线方程.

五、（10分）求微分方程 满足初始条件 的特解.

六、（10分）求幂级数 的收敛域（含端点）及和函数，并由此计算级数 的和.

七、（9分）计算曲线积分 ，其中L为从点A(0, 1)沿圆周 到点B(1, 2)的一段曲线.

八、（9分）计算曲面积分 ，其中S为曲面 的上侧.

九、（9分）求曲面 与曲面 所围立体的表面积.

注意：下面第十题(A)(B)两题只选做一题.（(B)题供H班学生选做）

十、（7分）

(A) 设 ，求证：

（1） 绝对收敛； （2）数列 收敛.

(B) 证明：函数项级数 一致收敛.