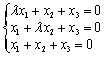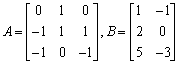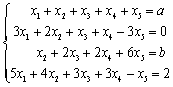2004级期末试题A

一、填空题(18分)

1. 设2阶矩阵 其中 均为2维列向量，且巳知行列式 则行列式 .

2. 设向量 垂直, 则 .

3. 齐次方程组 只有零解, 则 应满足的条件是 .

4. 设4阶矩阵 的秩为2, 则 的伴随矩阵 的秩为

5. 方程 所确定的曲面形状称为 .

6. 若二次型 是正定的，则 的取值范围是 .

二、(10分) 巳知矩阵 ，

求满足矩阵方程 的矩阵

三、(10分) 计算 阶行列式：

四、(10分) 设 是三阶方阵，且行列式 ，求行列式 的值，其中 是 的伴随矩阵.

五、(11分) 巳知线性方程组 为何值时方程组有解？当方程组有解.时，求出方程组的通解.

六、(10分) 在平面 内作一直线 ，使 通过直线 与平面 的交点 , 且 垂直于巳知直线 ，试求直线 的方程 .

七、(15分) 巳知二次型 .

用正交变换把二次型化为标准型，并求出相应的正交矩阵.

八、(8分) 设 阶矩阵 的元素全为1， 为单位矩阵，证明：矩阵 可逆，且

.

九、(8分) 设向量组 是齐次线性方程组 的一个基础解系，向量 不是方程组 的解，即 .试证明：向量组 线性无关.