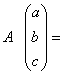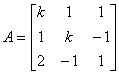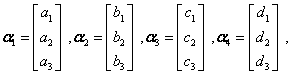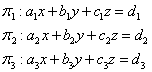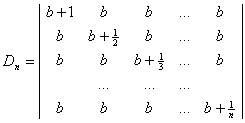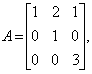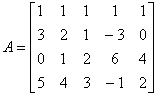2004级期末试题(B)

一、填空题（15分）

(1) 设 , .则矩阵A= ；

(2) 设 为三维列向量，巳知行列式 ，则行列式

(3)
设A, B为两个三阶方阵，且 ， 则

(4) 设 ，若方程组AX=O有非零解，则 k= ;

(5) 设向量 与向量 =（2， ，2）平行，且 ，则 = ..

二、填空题（15分）

(1) 设三角形的顶点为原点O及A=（1，2， ）, B=（1，1，0），则

外积 ，面积 ………………………………………… （ ）。

（A） ； （B） ； （C） ； （D） .

(2)设A、B都是 阶非零矩阵，且 ，则A和B的秩…………………… （ ）.

（A）必有一个等于零；（B）都等于 ；（C）一个小于 ，一个等于 ；（D）都小于 .

(3)设A是3阶可逆矩阵，且满足 ， （ 为A的伴随矩阵），则A的三个特征值是……………………………………………………………………… （ ）.

（A）3，3， ； （B） ， ，2； （C）3， ， ； （D） ，2，2.

(4). 设 阶矩阵A的伴随矩阵 ，且非齐次线性方程组 有两个不同的解向量 ，则下列命题正确的是 …………………… （ ）

(A) 也是 的解； (B) 的通鲜为（ ）；

(C) 满足 的数 必不为零； (D) 是 的基础解系.

(5).设

则三个平面 两两相交成三条平行线的充要条件是 …………… （ ）

(A) 秩 ;

(B) ;

(C) 中任意两个均线性无关，且 不能由 线性表出;

(D) 线性相关，且 不能由 线性表出.

三、（8分）计算行列式：

四、（8分）

设矩阵 解矩阵方程X=A+X B。

五、（8分） 求矩阵A的秩：

六、（10分）设直线 满足条件：（1）通过点 ( 0,2,2 );（2）平行于平面 ： ，（3）与直线 相交；求直线 的方程。

七、（7分）设方阵A满足 ，求证： 可逆，并求出 .

八、（10分）设方阵A的行列式 ，且 （其中 为 的伴随矩阵， 为 的转置矩阵），求证： 为零矩阵

九、（9分）设向量组 ， ，…， 是齐次线性方程组 的一个基础解系，向量 不是方程组 的解，即 ，试证明：向量组 ， ， ，…， 线性无关.

十、（9分）已知三元二次型 经正交变换化为 ，又知 ，其中 ， 为A的伴随矩阵，求此二次型的表达式.