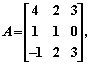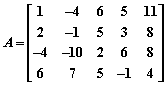2004级期中试题

一、选择题或填空题（40分）

(1) 设 为n阶方阵，满足 ，则必有（ ）.

（A） ；（B） ；

（C） 或 ；（D） 或.

(2) 设A, B为两个三阶方阵，且 ， 则

(3) 设 为三维列向量，巳知行列式 ，则行列式

(4) 设 为n阶方阵，则 可逆的充分必要条件是秩

(5) 设 为3阶方阵，秩 , 为 的伴随矩阵, 则秩

(6) 设向量 与向量 =（2， ，2）平行，且 ，则 =.

(7) 巳知向量 的模为 ， ，且 ，则

(8) 设原点O及点A（1，2， ）, 点 B（1，1，0），则外积

(9) 设有直线 与平面 ，

则两者的位置关系是（ ）

（A） ：（B） ；（C） 在 上；（D） 与 斜交.

(10) 设n阶方阵A、B、C满足关系式ABC=I，其中I为单位径矩阵，则必有（ ）..

（A）ACB= I；（B）CBA= I；（C）BAC= I；（D）BCA= I. .

二、（10分）计算行列式：

三、（12分）设矩阵 解矩阵方程AX = A +2 X .

四、（10分）求矩阵A的秩 .

五、（12分）试求点 ( 2,2,4 )关于平面 ： 的对称点 的坐标。

六、（8分）设A为n阶方阵, 满足 ，求证 可逆，并求出 .

七、（8分）设A为n阶非零方阵, 为 的伴随矩阵， 为 的转置矩阵, 当 时，证明：行列式