| 2006级期末试题A |
||||
|
一. 填空题(21分): 1. 设3阶矩阵A满足| A | = 2, 则
2. 设三角形的顶点为原点O及A = (1, 2,
面积
3.
4. R3中, 方程
5.
6. 若二次型
7. 设
二(8分). 计算行列式
三(8分). 求直线
四(10分). 已知
五(10分). 非齐次方程组的增广矩阵
六(12分). 用正交变换化二次型
注意: 在第七、第八题中任选做一题! 七(7分). 在
八(7分). 设
九(6分). 已知三阶矩阵A的特征值为
十(10分). 设
十一(8分). 已知矩阵
|
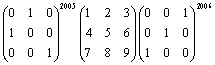 =_______.
=_______.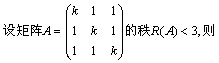 k = _________.
k = _________.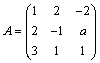 (a
(a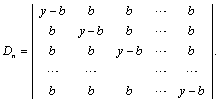
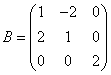 ,
, 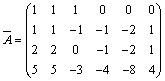 ,
,