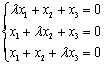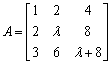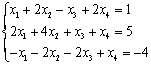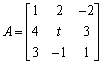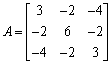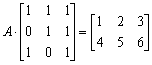线性代数与空间解析几何模拟试题2

一、填空题（每小题4分，共20分）

1． 设矩阵 ， ，其中 ， ，

， 均为3维列向量，且 ， ，

则 .

2． 设A是n阶矩阵且 ，

则 .

3． 设方程组 有非零解，

则 .

4． 设A是秩为2的3阶实对称矩阵，且 ，

则A的特征值为 .

5． 设 是正定二次型，

则a的取值范围是 .

1．当 （ ）时，矩阵 的秩为1.

（A）1，（B）2， （C）3， （D）4.

2．设 可由线性无关向量组 线性表示，

则r与s的关系（ ）.

（A） ， （B） ，

（C） ， （D）r与s无关.

3．设A，B都是n阶矩阵，则（ ）.

（A） 或 ，

（B） 且 ，

（C） 或 ，

（D） 且 .

4．设A、B均为n阶实对称矩阵，则A与B合同的

充要条件是（ ）.

（A）A、B有相同的特征值，

（B）A、B有相同的秩，

（C）A、B有相同的行列式，

（D）A、B有相同的正负惯性指数.

5． 在 中表示的图形是（ ）.

（A）椭圆， （B）双曲线，

（C）椭圆柱面， （D）双曲柱面.

三、（10分）求非齐次方程组的通解：

四、（10分）设平面 与 ： 垂直，

且与 的交线落在 平面上，求 的方程.

五、（10分）设n阶矩阵A的任何一行元素的和都是a，

求A的一个特征值与特征向量.

六、（10分）设 ，B为3阶非零矩阵且

，求t的值.

七、（10分）设矩阵 ，求可逆矩阵

P与对角阵 ，使 .

八、（8分）设A是n阶正定矩阵， 是非零

实n维列向量，且 （ ），

证明： 线性无关.

九、（7分）已知 ，求A.