第十三章 光 的 干 涉
思考题
13-1如图所示，波长为λ的单色平行光垂直入射到折射率为n2、厚度为e的透明介质薄膜上，薄膜上下两边透明介质的折射率分别为n1和n3，已知n1<n2， n2>n3，则从薄膜上下两表面反射的两光束的光程差是( )
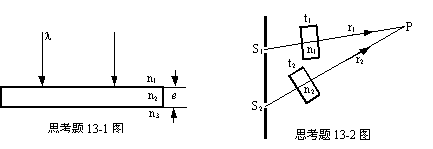
(A)2en2。 (B) 2en2+
。
(C) 2en2-λ。
(D) 2en2+
。
13-2如图，S1、S2是两个同初相的相干光源，它们到P点的距离分别为r1和r2。两光路中各有一块透明介质，其厚度和折射率分别为t1、n1和t2、n2，其余部分可看作真空，则从S1、S2发出的两光线到达P点的光程差等于( )
(A)(r2+n2t2)-(r1+n1t1)。
(B) (r2-t2+n2t2)-(r1-t1+n1t1)。
(C) (r2-n2t2)-(r1-n1t1)。
(D) n2t2-n1t1。
13-3 来自不同光源的两束白光，例如两束手电筒光，照射在同一区域内，是不能产生干涉花样的，这是由于（ ）
(A) 白光是由许多不同波长的光构成的。
(B) 来自不同光源的光，不能具有正好相同的频率。
(C) 两光源发出的光强度不同。
(D) 两个光源是独立的，不是相干光源。
13-4在相同的时间内，一束波长为λ的单色光在真空中和在玻璃中( )
(A) 传播的路程相等，走过的光程相等。
(B) 传播的路程相等，走过的光程不相等。
(C) 传播的路程不相等，走过的光程相等。
(D) 传播的路程不相等，走过的光程不相等。
13-5在双缝干涉实验中，为使屏上的干涉条纹间距变大，可以采取的办法是( )
(A)使屏靠近双缝。
(B)使两缝的间距变小。
(C)把两个缝的宽度稍微调窄。
(D)改用波长较小的单色光源。
13-6用白光光源进行双缝实验，
若用一个纯红色的滤光片遮盖一条缝，
用一个纯蓝色的滤光片遮盖另一条缝，
则( )
(A)干涉条纹的宽度将发生改变。
(B)产生红光和蓝光的两套彩色
干涉条纹。
(C)干涉条纹的亮度将发生改变。
(D)不产生干涉条纹。
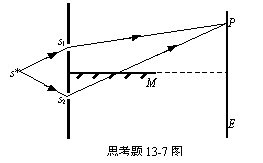
13-7在双缝干涉实验中，屏幕E上的P点处是明条纹。若将缝S2关闭，并在S1S2连线的垂直平分面处放一反射镜M，如图所示，则此时( )
(A) 屏幕E上的干涉条纹没有任何变化。
(B) P点处仍为明条纹。
(C) P点处为暗条纹。
(D)干涉条纹消失。
13-8在双缝干涉实验中，入射光的波长为λ，用玻璃纸遮住双缝中的一条缝，若玻璃纸中的光程比相同厚度的空气的光程大2.5l，则屏上原来的明纹处（ ）
(A) 仍为明条纹。
(B) 变为暗条纹。
(C) 既非明条纹，也非暗条纹。
(D) 无法确定是明条纹还是暗条纹。
13-9一束波长为λ的单色光垂直入射到置于空气中的透明薄膜上，薄膜的折射率为n，要使反射光得到加强，则薄膜的最小厚度是( )
(A)λ/4。 (B)λ/(4n)。 (C)λ/2。 (D)λ/(2n)。
13-10两块平板玻璃构成空气劈尖，左边为棱边，用单色平行光垂直入射。若上面的平板玻璃以棱边为轴，沿逆时针方向作微小转动，则干涉条纹的( )
(A)间隔变小，并向棱边方向平移。
(B)间隔变大，并向远离棱边方向平移。
(C)间隔不变，向棱边方向平移。
(D)间隔变小，并向远离棱边方向平移。
13-11波长为l的单色光垂直照射折射率为n2的劈尖薄膜（如图）,图中各部分折射率的关系是n1< n2 <n3。观察反射光的干涉条纹，从劈尖顶开始向右数第5条暗条纹中心所对应的膜厚e=（ ）
(A)
。
(B)
。
(C)
。
(D)
。
13-12用单色光垂直照射在如图所示的牛顿环装置上，当平凸透镜垂直向上缓慢平移而远离平面玻璃时，可以观察到这些环状干涉条纹（ ）
(A) 向右平移。 (B) 向中心收缩。
(C) 向外扩张。 (D) 静止不动。
(E) 向左平移。
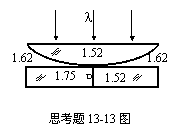13-13在图示三种透明材料构成的牛顿环装置中（图中的数字为相应媒质的折射率），用单色光垂直照射，在反射光中看到干涉条纹，则在接触点P处形成的圆斑为( )
(A) 全明。
(B) 全暗。
(C) 左半部明，右半部暗。
(D) 左半部暗，右半部明。
13-14 在迈克耳逊干涉仪的一支光路中放入一片折射率为n的透明介质薄膜后，测出两束光的光程差的改变量为一个波长λ，则薄膜的厚度是( )
(A)λ/2。 (B)λ/(2n)。 (C)λ/n。 (D)λ/[2(n-1)]。
三 习题
13-1 在杨氏双缝实验中，设两缝之间的距离为
13-2 在图示的双缝干涉实验中，若用薄玻璃片(折射率n1=1.4)覆盖缝S1，用同样厚度的玻璃片(折射率n2=1.7)覆盖缝S2，将使屏上原来未放玻璃时的中央明条
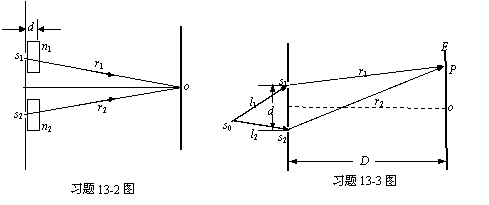
13-3 在双缝干涉实验中，单色光源S0到两缝S1和S2的距离分别为l1和l2，并且l1-l2=3λ，λ为入射光的波长，双缝之间的距离为d，双缝到屏幕的距离为D，如图所示。求： (1)零级明纹到屏幕中央o点的距离;
(2)相邻明条纹间的距离。
13-4 人造水晶钻戒是用玻璃(折射率为1.50)作材料，表面镀上一层一氧化硅薄膜(折射率n2=2.0)以增强反射。要使λ=5600Å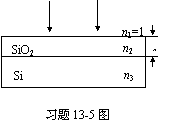
的光垂直入射时反射增强，求镀膜的厚度。
13-5在制造半导体元件时，常常需要在硅片(Si)上均匀涂上一层二氧化硅(SiO2)薄膜。已知SiO2的折射率为n2=1.5，Si的折射率为n3=3.4。在白光(400nm¾760nm)照射下，垂直方向上发现反射光中只有420nm的紫光和630nm的红光得到加强。
(1) 求二氧化硅(SiO2)薄膜的厚度；
(2) 问在反射光方向上哪些波长的光因干涉而相消；
(3) 如在与薄膜法线成30º角的方向上观察，白光中哪些颜色的光加强了？
13-6 一平面单色光垂直照射在厚度均匀的油膜(折射率n2=1.30)上，油膜覆盖在玻璃板(折射率为1.50)上。若单色光的波长可由光源连续可调，可观察到500nm和700nm这两个波长的光在反射中消失，而这两波长之间无别的波长发生相消，求此油膜的厚度。
13-7 由两块平板玻璃构成的一密封气体劈尖，在单色光垂直照射下，形成4001条暗纹的等厚干涉。若将劈尖中气体抽去，则留下4000条暗纹。求这种气体的折射率。
13-8 波长l1=500nm的单色光垂直照射到由两块光学平板玻璃构成的空气劈尖上，在反射光中观察，距劈尖棱边l=
(1)求此空气劈尖的劈尖角θ；
(2)改用l2=600nm的单色光垂直照射此劈尖，仍在反射光中观察，A处是明条纹还是暗条纹?
(3)在第(2)问的情形，从棱边到A处的范围内共有几条明纹?几条暗纹?
13-9 在牛顿环装置的平凸透镜和平板玻璃之间充满折射率n2=1.33的透明液体(设平凸透镜和平板玻璃的折射率都大于1.33)。凸透镜的曲率半径R=
(1)从中心向外数第十个明环所在处的液体厚度e10=？
(2)第十个明环的半径r10=？
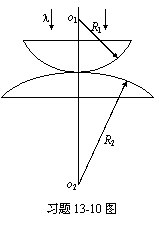13-10 两平凸透镜，凸球面半径分别为R1和R2，两凸面如图放置，凸面中心刚好接触。现用波长为l的单色光垂直入射，可以观察到环形的干涉条纹，求明暗条纹的半径。
13-11平板玻璃(折射率1.50)上放一油滴(折射率n2=1.20)，当油滴在重力的作用下展开成圆形油膜时，用波长λ=6000Å的平行单色光垂直照射，在反射光中观察干涉条纹。问：
(1)当油膜中心最高点与玻璃板上表面相距h=12000Å时，可看见几条明纹？明纹所在处的油膜厚度是多少？
(2)当油膜继续扩展时，所看到的条纹将如何变化？
13-12 (1)当迈克耳逊干涉仪的反射镜M1移动距离d=
(2)当在迈克耳逊干涉仪任一臂的光路中插入一薄玻璃片时，可观察到有150条干涉条纹向一方移过。若玻璃片的折射率n=1.632，所用单色光的波长λ=5000Å，求玻璃片的厚度e。