第四章
振动学基础
思考题
4-1什么是简谐振动？试分析以下几种运动是否是简谐振动？
(1)拍皮球时球的运动；
(2)一小球在半径很大的光滑凹球面底部的小幅度摆动；
（3）一质点分别作匀速圆周运动和匀加速圆周运动，它在直径上的投影点的运动。
4-2如果把一弹簧振子和一个单摆拿到月球上去，振动的周期如何改变？
4-3什么是振动的相位？一个弹簧振子由正向最大位移开始运动，这时它的相位是多少？经过中点，到达负向最大位移，再回到中点向正向运动，上述各处相应的相位各是多少？
4-4一个简谐振动的振动曲线如图所示。此振动的周期为（ ）
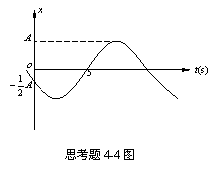(A)12s； (B)10s；
(C)14s； (D)1 1s。
4-5一个质点作简谐振动，振幅为A，
在起始时刻质点的位移为 A/2,且向x轴的
正方向运动；代表此简谐振动的雄转矢量
图为（ ）
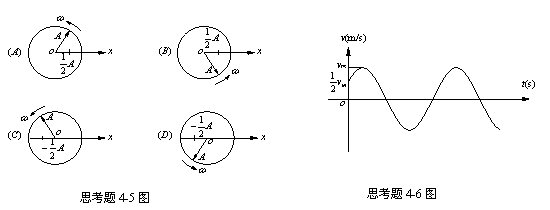4-6一质点作简谐振动，其运动速度与时间的曲线如图所示，若质点的振动规律用余弦函数描述，则其初位相应为（ ）
(A)π／6；（B） 5π/6；（C）-5π/6；（D）-π／6；
4-7把单摆从平衡位置拉开，使摆线与竖直方向成一微小角度θ,然后由静止放手任其振从放手时开始计时，若用余弦函数表示其运动方程，则该单摆振动的初位相为（ ）
(A)θ； (B) π； （C）0； （D π/2。
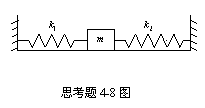4-8如图所示，质量为m的物体由倔强系数为k1和k2的两个轻弹簧连接，在光滑导轨上作微小振动,则系统的振动频率为（）
（A）
（B）
（C）
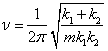（D）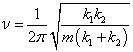
4-9一倔强系数为k的轻弹簧截成三等分，取出其中的两根，将它们并联在一起，下面挂一质量为m的物体，如图所示。则振动系统的频率为（ ）
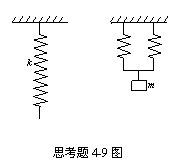(A)
(B)
(C)
(D)
4-10一弹簧振子作简谐振动，总能量为E1，
如果简谐振动振幅增加为原来的两倍，重物的
质量增为原来的四倍，则它的总能量E1变为（ ）
(A) E1/4; (B) E1/2； (C)2E1; (D) 4 E1。
4-11一质点作简谐振动，周期为T。当它由平衡位置向x轴正方向运动时，从二分之一最大位移处到最大位移处这段路程中所需要的时间为（ ）
(A)T/4； (B)T/12； (C)T/6; (D)T/8。
4-12一长为l，倔强系数为k的均匀轻弹簧分割成长度分别为l1和l2,的两部分，且
l1=n l2，n为整数，则相应的倔强系数k1和k2为（ ）
(A)
(B)
(C)
(D)
习题
4-1质量为
kg的小球与轻弹簧组成的系统，按 
(SI)
的规律作振动。求:
(1)振动的角频率、周期、振幅、初相、最大速度及最大加速度；
(2)t=1s，2s，5s，10s等各时刻的相位；
(3)分别画出该振动的x-t图线、v-t图线和a-t图线。
4-2有一轻弹簧，当下端挂一个质量ml=l
m2的振动周期和振动的数值表达式。
4-3一质点作简谐振动，其振动方程为
(SI)
试用旋转矢量法求出质点由初始状态
(t=0的状态)运动到x=
所需最短时间∆t。
4-4一个轻弹簧在60N的拉力作用下可伸长
（1）此小物体是停在振动物体上面还是离开它？
(2)如果使放在振动物体上的小物体与振动物体分离，则振幅A需满足何条件？两者在何位置开始分离？
4-5一物体放置在平板上，此板沿水平方向作谐振动。已知振动频率为2Hz，物体与板面最大静摩擦系数为0.5。问：要使物体在板上不发生滑动，最大振幅是多少？
4-6一台摆钟的等效摆长l=
4-7一弹簧振子沿x轴作简谐振动，已知振动物体最大位移为xm= 
，又知t=0的初位移为＋
(1)求振动能量；
（2）求此振动的表达式。
4-8已知两个在同一直线上的简谐振动的振动方程分别为
(SI)
(SI)
（1）求它们合成振动的振幅和初相；
(2)另有一同方向的简谐振动
(SI) 。问
为何值时，x1+x3的振幅为最大？为何值时x2+x3的振幅最小？(3)用旋转矢量图示法表示（1）、(2)两小题的结果。
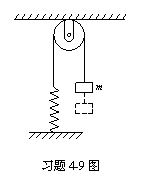
4-9一定滑轮的半径为R,转动惯量为J，其上挂一轻绳，绳的一端系一质量为m的物体，另一端与一固定的轻弹簧相连，如图所示，设弹簧的倔强系数为k，绳与滑轮间无滑动，且忽略轴的摩擦力及空气阻力，现将物体m从平衡位置拉下一微小距离后放手，证明物体作简谐振动，并求出其角频率。
4-10边长l = 0.l
（l）木块将作什么运动
(2)求木块质心（重心）运动规律的数值表达式。（水的密度ρ’=