第五章 波动学基础
思考题
5-1把一根十分长的绳子拉成水平，用手握其一端，维持拉力恒定，使绳端在垂直于绳子的方向上作简谐振动，则
（A）振动频率越高，波长越长；
（B）振动频率越低，波长越长；
（C）振动频率越高，波速越大；
（D）振动频率越低，波速越大。
5-2在下面几种说法中，正确的说法是
（A）波源不动时，波源的振动周期与波动的周期在数值上是不同的；
（B）波源振动的速度与波速相同；
（C）在波传播方向上的任二质点振动位相总是比波源的位相滞后；
（D）在波传播方向上的任一质点的振动位相总是比波源的位相超前
5-3一平面简谐波沿ox正方向传播，波动方程为
(SI)
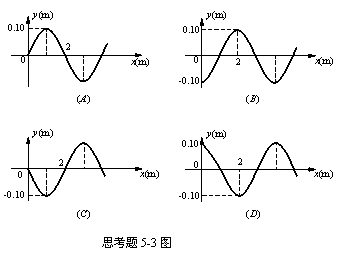
该波在t=0.5s时刻的波形图是（ ）
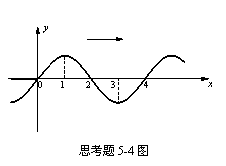
5-4图示为一沿x轴正向传播的平面
简谐波在t=0时刻的波形，若振动以余弦
函数表示，且此题各点振动初相取-π到π
之间的值，则（）
（A）1点的初位相为
1=0
（B）0点的初位相为0=-π/2
（C）2点的初位相为2=0
（D）3点的初位相为3=0
5-5一平面简谐波沿x轴负方向传播。已知x=b处质点的振动方程为
，波速为u，则振动方程为（ ）
(A)
(B)
(C)
(D) 
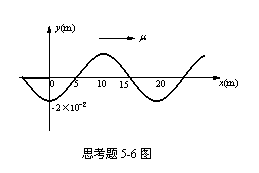
5-6一平面简谐波，波速u=
处的振动方程为（ ）
（A）
(SI)
（B）
(SI)
（C）
(SI)
（D）
(SI)
5-7一平面简谐波沿x轴正方向传播，t=0的波形曲线如图所示，则P处质点的振动在t=0时刻的旋转矢量图是（ ）
5-8当一平面简谐机械波在弹性媒质中传播时，下述各结论一哪个是正确的？
（A）媒质质元的振动动能增大时，其弹性势能减少，总机械能守恒；
（B）媒质质元的振动动能和弹性势能都作周期变化，但两者的位相不相同；
（C）媒质质元的振动动能和弹性势能的位相在任一时刻都相同，但两者的数值不相等；
（D）媒质质元在其平衡位置处弹性势能最大。
5-9一平面简谐波在弹性媒质中传播，在某一瞬时，媒质中某质元正处于平衡位置，此时它的能量是
(A)动能为零，势能最大；(B)动能为零，势能为零；
(C)动能最大，势能最大；(D)动能最大，势能为零。
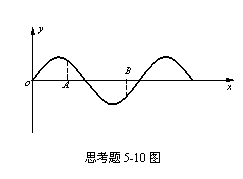5-10图示为一平面简谐机械波在t时刻的
波形曲线。若此时A点处媒质质元的振动动能
在增大，则
(A)A点处质元的弹性势能在减小；
(B)波沿x轴负方向传播；
(C) B点处质元的振动动能在减小，
(D)各点的波的能量密度都不随时间变化。
5-11一平面简谐波在弹性媒质中传播，在媒质质元从最大位移处回到平衡位置的过程中
(A)它的势能转换成动能；
(B)它的动能转换成势能；
(C)它从相邻的一段媒质质元获得能量，其能量逐渐增加；
(D)它把自己的能量传给相邻一段媒质质元，其能量逐渐减小。
5-12 S1和S2是波长为λ的两个相干波的波源，相距3λ/4，S1的位相比S2超前π/2，若两波单独传播时，在过S1和S2的直线上各点的强度相同，不随距离变化，且两波的强度都是I0，则在S1、S2连线上S1外侧和S2外侧各点，合成波的强度分别是
(A) 4 I0, 4 I0；(B) 0, 0；(C) 0, 4 I0；(D) 4 I0，0。
5-13在一根很长的弦线上形成的驻波是
(A)由两列振幅相等的相干波，沿着相同方向传播叠加而形成的；
(B)由两列振幅不相等的相干波，沿着相同方向传播叠加而形成的；
(C)由两列振幅相等的相干波，沿着反方向传播叠加而形成的；
(D)由两列波，沿着反方向传播叠加而形成的。
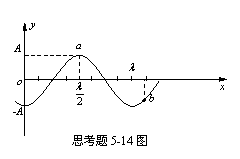
5-14某时刻驻波波形曲线如图所示，
则a、b两点的位相差是
(A) π (B) π/2 (C) 5π/4；(D)0。
5-15在弦线上有一简谐波，其表达式是
(SI)
为了在此弦线上形成驻波，并且在x=0处为一波节，此弦线上还应有一简谐波，其表达式为
（A）
(SI)
（B）
(SI)
（C）
(SI)
（D）
(SI)
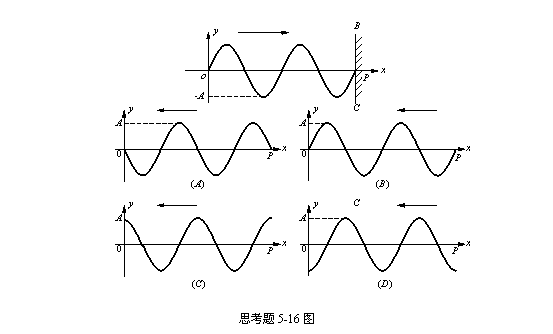
5-16如图所示，为一向右传播的简谐波在t时刻的波形图，BC为波密介质的反射面，波由P点反射，则反射波在t时刻的波形图为
习题
5-1一横波方程为 
式中A=0.
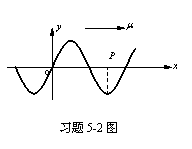
5-2一平面简谐波沿x轴正向传播，其振幅和角频率分为A和ω，波速为u，设t=0时的波形曲线如图所示。
(1)写出此波的波动方程。
(2) 求距o点分别为λ/8和3λ/8两处质点的振动方程。
(3)求距o点分别为λ/8和3λ/8两处质点在t=0时的振动速度：
5-3如图所示为一平面简谐波在t=0时刻的波形图，设此简谐波的频率为250Hz,且此时质点P的运动方向向下，求
(1)该波的波动方程；
(2)在距原点o为
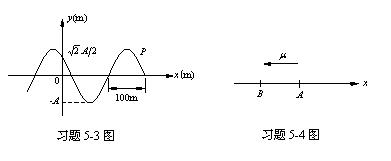
5-4如图，一平面波在介质中以速度u=
(SI)
(1)以A点为坐标原点写出波动方程；
(2)以距A点
5-5一平面简谐波在介质中以速度u=
(SI)
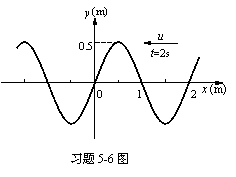另一点D在A点右方
(1)若取x轴方向向左，并以A为坐标原点，试写出波动方程，并求出D点的振动方程。
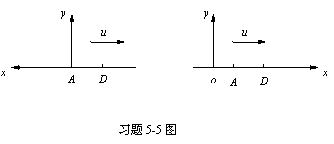
(2)若取x轴方向向右，以A点左方
5-6沿x轴负方向传播的平面简谐波在t= 2s时刻的波形曲线如图所示，设波速u=0.
5-7如图所示，一角频率为ω,振幅为A的平面简谐波沿x轴正方向传播，设在t=0时该波在原点o处引起的振动使媒质质元由平衡位置向y轴的负方向运动。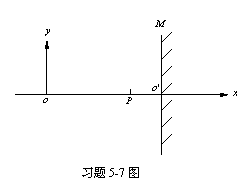
M是垂直于x轴的波密媒质反射面。己知
; 
(λ为该波波长)，设反射波不衰减，求：
（1）人射波与反射波的波动方程；
(2)P点的振动方程。
5-8一列横波在绳索上传播，其表达式为
(SI)
(1)现有另一列横波（振幅也是
(2)写出绳索上驻波方程；求出各波节的位置坐标表达式；并写出离原点最近的四个波节的坐标数值。
5-9如图所示。(1)当振动频率为2040Hz的声源S向墙壁运动时，在o点的观察者听到拍音频率n拍=3Hz。若声波在空气中的速度为c=
(2)若声源S不动，而以一可移动的反射面代替墙壁，反射面以速度v=0.
