 教研论文 1 2 教研论文 1 2
量子力学教学中的难点探讨
吴志明 张晓霞
电子科技大学光电信息学院 四川成都 610054
摘要:本文就量子力学教学中两个学习的难点,波动性、几率波概念的教学问题进行了探讨。
关键词:几率波,测不准关系。
中图法分类号: O413.1
量子力学的基本概念与我们的生活实际相去甚远,学生难于接受,所以成了物理学最难学的课程之一。 解决的办法需要从学生熟悉的知识入手,剥去量子力学基本概念的神秘面纱,还原这些概念的物理实质,再通过与经典物理类比,就会使学生对这些概念产生深刻的印象。基本概念的掌握能够促进对整个近代物理学的理解 [1-3] 。
当量子力学课程介绍完近代物理学实验遇到的困难之后,就必须面临如何向学生介绍微观粒子的波动性问题。尽管学生从近代物理实验中可以了解到微观粒子的波动属性,但对于微观粒子的作为波动和粒子性的统一体仍难以理解。这是因为与经典物理类比这些基本概念与我们的生活实际相去甚远。为了加深对于微观粒子波动性和几率波的概念的理解,有必要深入分析和讲解。
一、 几率波
早在 1926 年,波恩就提出和微观粒子相联系的德布罗意波是一种几率波。这一概念的提出意味着:几率波振幅的平方代表一个粒子在空间各点出现的几率密度,同时只有大量粒子的情况下,几率分布才能通过粒子数分布表现出来,所以几率波描述的是大量粒子的统计行为 [4] 。
用几率波当然很容易解释粒子的衍射实验,所谓粒子发生衍射,其实是粒子的几率波德布罗意波发生衍射,衍射后的几率波振幅的平方决定了粒子在各处出现的几率密度,几率密度大的地方投射的粒子多,几率密度小的地方投射的粒子也少,只有大量的粒子不管它们是同时被衍射的或者是一个接一个地发生衍射,最终都应产生相同的衍射图样。若问某个粒子将落到何处,则几率波的描述就不能回答了。所以几率波不能决定某个粒子将在何时何地出现,只能给出几率性的回答。采用几率波的概念,意味着我们认为“微观理论是统计性质的”。它不同于经典力学中对粒子的描述是“决定性的”。
几率波的概念核心是不涉及粒子的结构,当几率波发生变化时,改变的也是粒子在空间各点出现的几率,而不会改变粒子的结构。所以它和粒子性不矛盾。迄今为止,它仍然是一类对物质的波粒二象性所能提供的最好解释。进一步可以有以下描绘的图像加以说明 :
1.经典的波和粒子的概念不能说明波动性与粒子性
在经典物理中,粒子有确定的位置, 是 定域的;波是弥散的,分布在一定的空间里, 是非定域的。二者有许多根本不同之处,不能同时描述一个物体。用经典物理说明波动性与粒子性,只能认为波和粒子二者有一个是基本的,另一个由它组成,若认为波是大量粒子所组成的,则不能说明为何单个的微观粒子(指大量单个粒子的长时间行为)也有波动性,若认为粒子是波组成,则只有波包才能象粒子一样局限在很小的范围,波包是由不同频率的单色波线性叠加而成的,在媒质中传播时,各种单色波的速度不同,这意味着传播中波包即粒子会逐渐变大甚至消失,这显然是荒唐的,所以经典概念无法解释波粒二象性。
2.几率波不是经典波
熟知的经典波有机械波和电磁波,机械波是机械振动在媒质中的传播,电磁波是变化的电场和变化的磁场在空间的传播,总之都是某种物理量在空间的传播的结果,这些概念来自于经典物理的现象,它们的性质我们比较了解,这两种波也有区别,机械波的传播需要某种媒质,电磁波的传播不需要媒质。
几率波的概念来自于微观粒子的波动性,为了解释微观粒子的干涉和衍射等实验,才提出这样一种可以干涉和衍射但又与粒子性互不矛盾的波,干涉和衍射是几率波和经典波的共同之处。
通过与经典物理图像相比较 , 可给出微观粒子的波粒二象性只是说明微观粒子与经典的粒子和经典的波某些侧面有相似之处,但又与它们有原则区别的结论。
二、测不准关系与普朗克常数 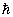
测不准关系:若两个力学量算符的对于关系为: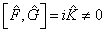 时,这两个力学量满 时,这两个力学量满
足下列关系: 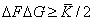 这一关系称为测不准关系。 这一关系称为测不准关系。
例 : 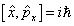 , 则 , 则 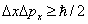
测不准关系可以严格的数学证明。微观粒子具有明显的波动与宏观粒子无明显波动的特点形成了鲜明的对照。这其中普朗克常数 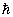 起了重要的作用,下面的例子可以说明这一点。 起了重要的作用,下面的例子可以说明这一点。
例: 在奇特的量子田地里,其中 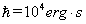 。瓜的直径近似 20cm ,且含有质量约 0.1g 的种子。问:当我们切开量子田地里长熟的瓜时 , 是幅怎样的图像 ? 在 628nm 波长光子的反射下瓜的反冲是多大 [5] 。瓜的直径近似 20cm ,且含有质量约 0.1g 的种子。问:当我们切开量子田地里长熟的瓜时 , 是幅怎样的图像 ? 在 628nm 波长光子的反射下瓜的反冲是多大 [5]
解:由测不准关系 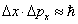
得到瓜的种子动量不确定量 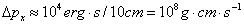
所以其速度不确定量 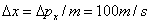
当瓜被切开时,种子就以这个(平均)速度离开瓜。
波长 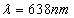 的光子有动量 的光子有动量 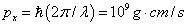 和能量 和能量 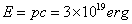 ,瓜的质量是 ,瓜的质量是 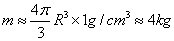 ,它的静能量是 ,它的静能量是 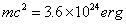 ,因此我们可用以非相对论性地计算。考虑弹性碰撞,碰后瓜的动量近似为 ,因此我们可用以非相对论性地计算。考虑弹性碰撞,碰后瓜的动量近似为 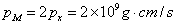 。相当于速度 。相当于速度 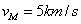 。这个速度小于由地球逃逸的速度.当光子被看见的时到,瓜已经处于别处。 。这个速度小于由地球逃逸的速度.当光子被看见的时到,瓜已经处于别处。
在这一例子中,其核心是假定将普朗克常数放大了 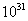 倍,将使得在宏观尺度里,出现明显的波动性 , 由不确定关系 倍,将使得在宏观尺度里,出现明显的波动性 , 由不确定关系 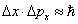 我们 可以看到,相应的 我们 可以看到,相应的 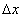 与 与 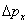 均也放大,从而出现这幅景象。而事实上,宏观领域的 均也放大,从而出现这幅景象。而事实上,宏观领域的 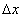 与 与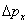 的乘积远远大于实际的普朗克常数,因此相比较而言,宏观领域的这种波动性可以忽略不计。 的乘积远远大于实际的普朗克常数,因此相比较而言,宏观领域的这种波动性可以忽略不计。
由此可以看到除了直接计算德布罗意波长与粒子的运动空间进行比较外 , 还可以从另一角度去理解微观粒子的波动性。通过这一比较,可以加深同学对量子力学基本概念的理解,从而提高量子力学课堂的教学的效果。
参考文献 :
1. 学习量子力学应注意的几个问题 高等函授学报 1995 年 5 期 p17-20
2. 试量子力学中的测不准关系 吴洪 广西物理 Vol.18 (1997):11-14
3. 浅谈量子概念的理解 胡响明 高等函授学报 2004 年 5 期 Vol.17 p29-32
4. 材料物理导论 恽正中 电子科技大学出版社 1995.8
5. 量子力学导论 [ 德 ] 瓦尔特 . 顾莱恩 北京大学出版社 2001 年 5 月 |