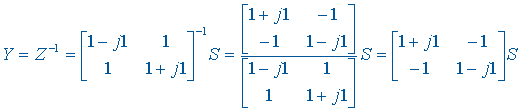| 1 |
 Homepage |
Exercise |
Old Test |
Download |
例10-9
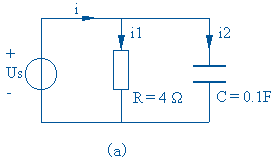
电路图中，已知 R＝4欧姆，C＝0.1F， 
试求
i1(t), i2(t), i(t) 及其有效值当量
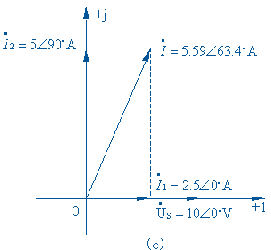
解：
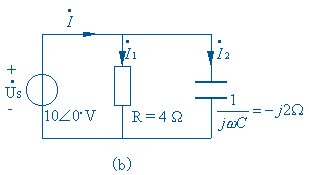
根据图 (a) 所示电路的时域模型，画出图( b )所示的相量模型，图中各电压、电流参考方向均与时域模型相同，仅将时域模型中各电压、电流符号 Us，i1，i2，i
用相应的相量符号
表示，并计算出电压相量
。根据 RLC 元件相量形式的 VCR 方程，计算出电流：
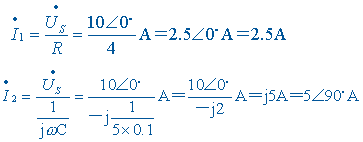
根据相量形式的 KCL 方程得到
根据所求得的各电压相量得到相应电压的瞬时值表达式：
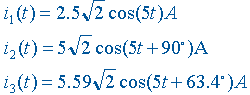
根据所求得的各电压电流相量画出相量图，图如
(c) 所示。由此图可以看出电流 i(t) 超 前电压 Us(t) 的角度为 63.4度。此例中，
，再次说明正弦 电流电路中流出任一结点的全部电流有效值的代数和不一定等于零。
例10-10
电路图如图，已知电感电流 
。试用相量法求电流
i(t) ，电压 u(t) 和 Us(t)。
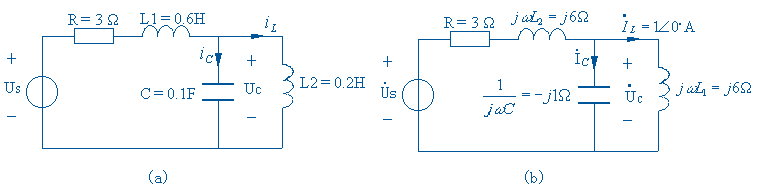
解： 1. 画出电路图 (a) 的相量模型如图 (b) 所示。其中：
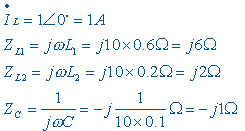
2. 观察相量模型，用相量形式的 KVL 和电感 VCR 方程求出电感电压和电容电压相量
根据相量形式的电容 VCR 方程求出电容电流相量
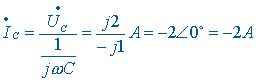
根据相量形式的 KCL 方程求出电阻电流相量
根据相量形式的 KVL 方程和电阻及电感 VCR 方程，求出电压源电压相量
根据电流相量 
，电容电压相量
和电压相量 
以及角 频率
，求得电流 i(t)，电压
Uc(t) 和 Us(t) 的瞬时表达式为：
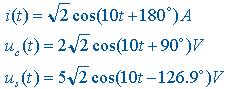
例10-11
已知如图电路的
试用相量方法计算 电路中的
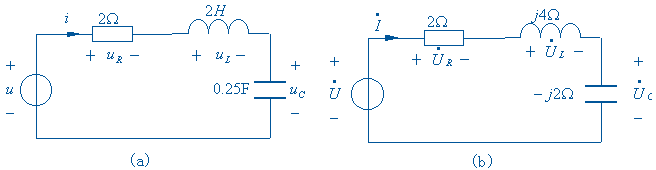
解： 图 (a) 中电路的相量模型，如图 (b) 所示。求出 RLC 串连电路的等效阻抗
求出 RLC 元件的相量电流
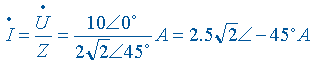
用 RLC 元件的欧姆定律或直接用分压公式计算 RLC 元件上的电压相量：
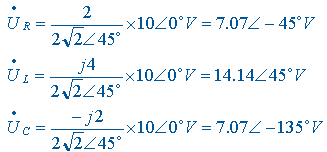
根据以上电压、电流相量得到相应的瞬时值表达式：
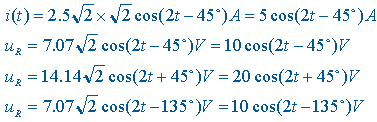
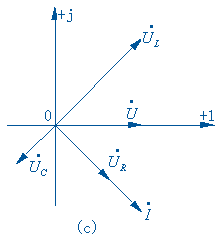
各电压、电流的相量如图( c )所示。从相量图上清楚地看出各电压、电流的相量关系，例如从端口电压
的相位超前与端口电流 
的角度为
表明 RLC 串连单口网络的端口特性等效于一个电阻与电感的串连，即单口网络具有电感性。从相量图还可以看出
其中电感电压
比总电压
还要大，这再次表明电压有效值之间不服从
KVL 定律。
例10-19
试求图 (a) 所示单口网络在
和
时的等效导纳。
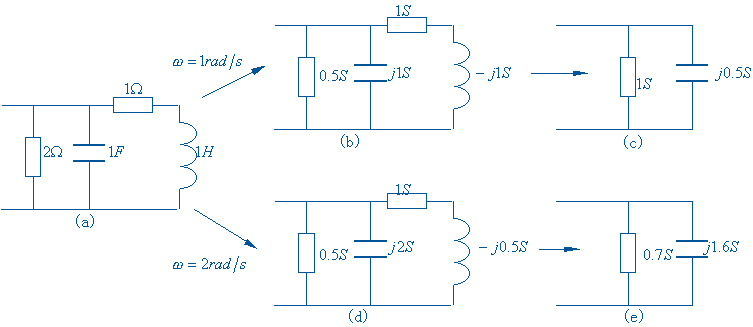
解
根据 (b) (c) 所示在
和 
时的相量模型可求出相应的等效导纳：
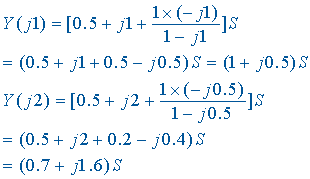
由等效导纳得到的等效电路如图 (c) (e)所示。
例10-23 电路图所示。问负载阻抗 
应该为何值式，电流
达到最大值。
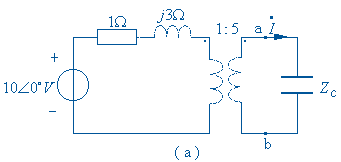
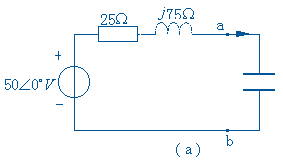
解
将连接负载阻抗
的单口网络用戴维宁等效电路代替。先求出带路电压
利用理想变压器的阻抗变换性质，求得单口网络的输出阻抗
得到(
b )所示电路，由此容易看出，当 
时得到最大电流为
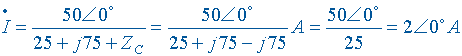
例10-24
图( a )所示双口网络工作于正弦稳态，觉频率
求其 Z 参数矩阵。
解
画出双口网络的相量模型如图( b )所示。在 Z 参数表达式中，电流 
是自变量， 可以将这两个电流做为激励信号，端口电压作为响应来看待，即在端口上外加两个电流源相 量
来计算端口相量
的表达式，从而得到
Z 参数矩阵。
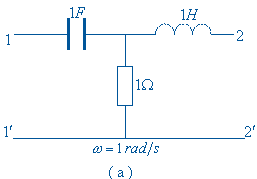
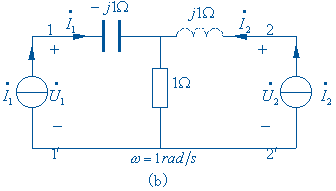
可以列出网孔方程
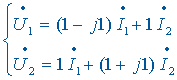
将此方程于 Z 参数方程对比，可以得到 Z 参数矩阵为
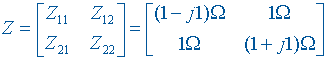
也可以用叠加定理分别求出四个
Z 参数，当
单独作用
，即次级开路时，可以求
得 
。当 
单独作用
，
即初级开路时可以求得
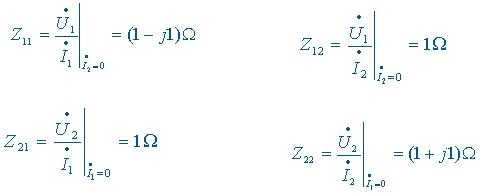
求得 Z 参数矩阵后，用求逆矩阵的方法可以得到 Y 参数矩阵。
| Homepage |
Exercise |
Old Test |
Download |
