|
分子运动实验
【实验目的】
利用钢球(代表气体分子)造成气体分子混乱运动模型,来模拟演示布朗运动、气体压强的统计意义、理想气体状态方程、实际气体状态方程、玻尔兹曼分布率等分子运动规律。
【实验器材】
分子运动演示仪,稳压电源,其结构如图74-1所示。
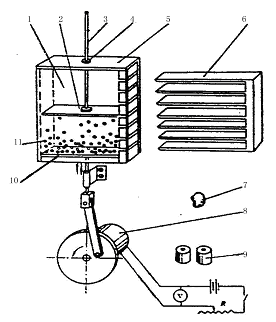
图74-1
1.透明方箱(有机玻璃制作),2.活塞,3.活塞杆,4.橡胶塞,5.盖板,6.多层插板,7.布朗粒子,8.直流电动机(转速可调,额定功率10W),9.砝码,10.振动板,11.钢球(直径1.5mm、数量约300粒)。
【实验操作与现象】
(1)把约300粒钢球放入模拟箱内,使钢球大体铺满箱底一层,再将布朗粒子(发泡塑料块)放入,这时把浮动活塞插入并盖上盖板。在活塞杆上套一带孔的橡胶塞,用它调节并固定浮动活塞在一定高度上(一般可在10—15cm高度)。
(2)接通电源,振子钢球在振板的撞击下(振子也相互碰撞)作混乱运动。调节电压可使振子混乱运动激烈程度变化。这时,可以看到布朗粒子在钢球(分子)碰撞下不断运动。由于布朗粒子形状不规则,实验中可看到布朗粒子边转边移动,形成明显的布朗运动。
2.气体压强统计意义的演示
(1)实验原理
理论研究表明,气体压强可由分子对某一面(如器壁)碰撞造成的冲量变化求出,而每一瞬间哪些分子碰撞器壁,碰撞时传给器壁冲量的大小,都具有偶然性,因而反映大量分子碰撞冲量的统计平均(气体压强)必有起伏。起伏的大小与分子数有关(起伏与1/n成比例),当分子密度n小时,其起伏就大;而分子数密度n大时,其起伏小。利用分子运动理论演示器就可以演示气体压强的这种统计意义。
(2)实验操作
在方箱中装几十个振子,这时振板使少量振子振动造成的压强值就很不稳定,实验时我们看到浮动活塞上下起伏很大;当方箱中放入大量振子时,就会看到有一个稳定的压强值,这时浮动活塞在大量振子的撞击下处于某一位置,起伏很小。
3.理想气体状态方程的演示
利用分子运动理论关于理想气体模型的假设,可推导出理想气体的状态方程,即
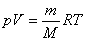 或 或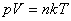 (74-1) (74-1)
对于一定质量(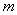 一定或总分子数 一定或总分子数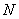 一定)的理想气体,从其状态方程可知,当温度 一定)的理想气体,从其状态方程可知,当温度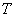 一定时,气体压强 一定时,气体压强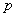 与分子数密度 与分子数密度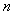 成正比。 成正比。
在模拟箱中放入振子约300粒,即分子总数N=300个,如图74-2所示。在电机额定转数情况下,由于振板的撞击造成振子的混乱运动,产生一定压强(由浮动活塞的重量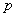 表示),这时可测得浮动活塞在 表示),这时可测得浮动活塞在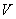 位置;在电机额定转数不变情况下,这相当于保证温度 位置;在电机额定转数不变情况下,这相当于保证温度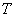 恒定(即造成的振子混乱运动激烈程度不变),用备制的砝码将活动活塞重量增加一倍,这时压强变为 恒定(即造成的振子混乱运动激烈程度不变),用备制的砝码将活动活塞重量增加一倍,这时压强变为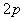 ,可测得浮动活塞在 ,可测得浮动活塞在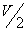 位置;当压强为 位置;当压强为 时,测得容积为 时,测得容积为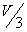 。 。
由此可知,当压强为 时,相应的分子密度 时,相应的分子密度 ;当压强为 ;当压强为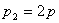 时, 时,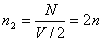 ;当压强为 ;当压强为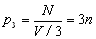 ;可见,在温度一定(电机转速一定)时,压强与粒子数密度成正比,即 ;可见,在温度一定(电机转速一定)时,压强与粒子数密度成正比,即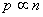 。 。
4.实际气体状态方程的演示
(1)实验原理
对于钢球模型,实际气体状态方程可写为:
 (74-2) (74-2)
式中 为气体质量, 为气体质量,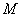 为气体摩尔质量, 为气体摩尔质量, 为一修正值, 为一修正值, 是钢球振子本身的体积。本演示仪可在电机额定功率下(对应温度 是钢球振子本身的体积。本演示仪可在电机额定功率下(对应温度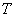 一定)通过实验求得 一定)通过实验求得 ,从而演示实际气体状态议程。 ,从而演示实际气体状态议程。
(2)演示方法
在模拟箱中铺满一层钢球振子(300粒),令电机在某一额定转速下,造成浮动活塞在A位置,如图74-2所示。保证电机额定转速不变,用备制砝码使浮动活塞加重一倍,是活塞达到B位置。按理想气体考虑,在温度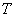 及粒子数 及粒子数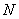 一定情况下,气体压强和体积之积为一常量,即pV=常量 一定情况下,气体压强和体积之积为一常量,即pV=常量
本实验对应的情况是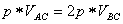
则

图74-2
而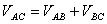
故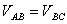
依上所述计算,图中C线上面的容积正是理想气体分子活动的容积,而C线下到振板(居中位置)的容积 则是实际气体分子(钢球振子)本身有一定体积所造成的体积修正量。实验测出的大小,再与钢球振子( 则是实际气体分子(钢球振子)本身有一定体积所造成的体积修正量。实验测出的大小,再与钢球振子(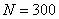 粒)本身体积 粒)本身体积 相比,计算结果表明: 相比,计算结果表明:
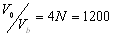 ( 74-3)
( 74-3)
由此可见,考虑到分子本身体积的影响,实际气体分子活动容积应为 ,这样就演示了一种气体的状态方程。 ,这样就演示了一种气体的状态方程。
5.玻尔兹曼分布律的演示
(1)实验原理
在重力场中理想气体分子数密度按高度服从玻尔兹曼分布律,即
 (74-4)
(74-4)
(2)演示方法:
1)在模拟箱中放入振子300粒(或更多此),盖好盖板,并把分子数分离隔槽(多层插板)端头插在有缝隙的箱挡板中。
2)调整电压(一般不必太大,如5V)使振子振起来,这时大量振子在重力场中按高度形成一定分布。稳定片刻后,迅速用手把多层插板插入模拟箱之中,此时振子就被分离隔槽分割在不同高层里。关掉电源。
3)把方箱向右侧倾斜,各层的振子钢球则在各自的隔槽中排布起来。
观测各层粒子数的多少,从隔槽的第一层起,画一曲线,可以看出该曲线随着高度按 的负指数衰减,从而演示了玻尔兹曼分布律。 的负指数衰减,从而演示了玻尔兹曼分布律。 |


